Inscription / Connexion Nouveau Sujet
ensemble des points
Bonjours a tous.. et bonne année 2008 a tous..
j'ai un dm a rendre pour la rentrée mais je suis un peu bloqué dessus..
est-ce que vous pouriez m'aider =)
merci d'avance
voila les énoncés:
1) ABC est un triangle de cotés AB = 6 , AC = 4 et BC = 8. Determiner les ensembles de points suivants. Representer ces ensembles
I={M(x;y):||2MA-3MB+4MC||=||2MA+MB||}
J= M: ||MA+3MB+4MC||=||MA-MB||
2) A, B et C sont 3 points distincts. Determiner les ensembles de points suivant. Representer ces ensembles :
K = (M: (AM;AB) =  /6 [2
/6 [2 ]
]
L = M : (AM;BA) =  /2
/2
... il y en a d'autre mais si on me donne des exemples je pense que je peux faire les autres
merci beaucoup...
Bonjour,
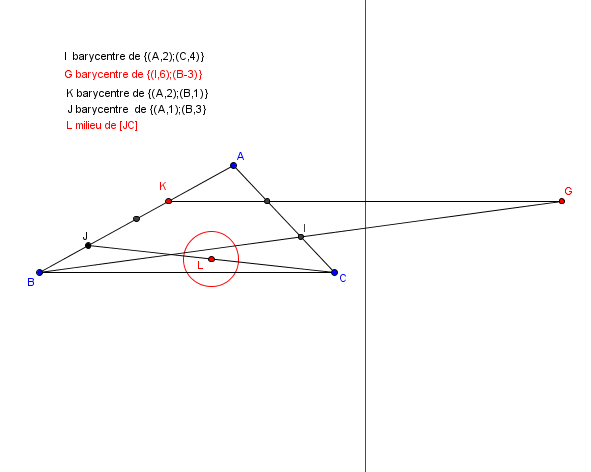
1) Soit le barycentre de
et le barycentre de
La première relation s' écrit:
soit
Le lieu cherché est donc la médiatrice de
Soit le barycentre de
La seconde relation s' écrit:
soit:
Le lieu cherché est donc le cercle de centre et derayon

Bonjour a tous j'ai un exercice a faire mais je sais pas comment m'y prendre vous pouriez me donner quelques piste ^^
l'exercice est :
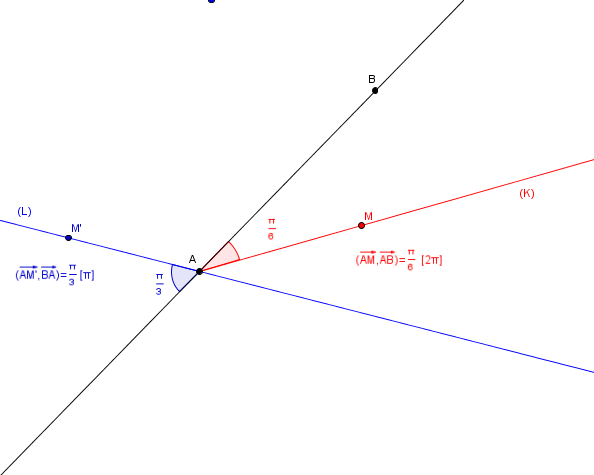
A, B et C est 3 points distincts. Determiner les ensembles de points suivants
K={M: (AM,AB)= pi/6 [2pi]
L={M: (AM,BA)= pi/3 [pi]
il y en a d'autres mais si vous m'aidiez pour les deux je pense que je peux finir les autres ...
Merci d'avance
*** message déplacé ***
merci pour la premiere question mais je voudrais savoir comment je dois faire l'autre exercice ^^
s'il vous plait il y aurait quelqu'un pour m'aider ??
Re,
L' ensemble cherché est la demi droite issue de
:
tel que
et privée du point
Pour , on est modulo
Il s' agit de la droite passant par de vecteur directeur
tel que
privée de
.
Mais c' est plus facile avec un dessin...

mais je vois pas comment vous avez trouvé..
pouriez vous m'expliquer 
ok je pense avoir compris merci
mais j'en ai d'autre mais je n'avais pas fais attention que les lettres n'était pas le meme ^^'
P= M (MA,MB) = pi/2 [2pi]
comment je dois le faire ?
Un dessin:
Dessine un cercle de diamètre
Tu remarques que suivant que est d' un côté où de l' autre du diamètre surle cercle,
ou
Le lieu cherché est donc un des 2 demi cercles privé des points A et B (celui tel que l' angle soit compté positivement en allant de vers
)

et pour
P= M (MA,MB) = pi/2 [pi]
c'est pareil no ?
Là, l' angle orienté peut valoir
puisque l' on est modulo
Il s' agit donc du cercle de diamètre tout entier privé des points
et

enfait je vous toujours pas la différence entre modulo pi et 2pi
je suis desolé je prends beaucoup de temps pour comprende
non finalement j'ai compris merci beaucoup "cailloux"
Un exemple:
Si ,
Cela signifie que avec
en prenant , on obtient sucessivement:
Si ,
Cela signifie que avec
en prenant , on obtient sucessivement:
Tu peux essayer de les reporter sur un cercle trigonométrique...