Inscription / Connexion Nouveau Sujet
mais, comme jeveuxbientaider, je suis étonnée que l'on te demande de montrer l'alignement de ces 3 points qui ne sont jamais alignés quand on déplace M ... !!! ... ??? !!! ...
Mais alors pourquoi avoir trouvé ma question débile quand j'ai demandé si je devais, pour M, exprimer y en fonction de x dans l'équation de cercle?
Et si on ne conclut pas à l'alignement des points je ne vois pas trop l'objectif de tous ces calculs!!!
je poursuis la vérif des calculs:
x1 : erreur de signes !
y1 à reprendre, donc
x2 et y2 , c'est juste
x3 et y3 aussi, mais pour y3, simplifie par 2 !
calculer les coordonnées des vecteurs, ce n'est pas un pb, tu appliques le cours
mais le vrai pb, c'est qu'il n'y a pas alignement (en tout cas, pas qq soit n!)
ok
de mon coté je mène les calculs "au bout", pour voir où ça mène et parce que j'ai du temps à perdre et parce que je suis curieuse 
la relation entre x et y, si elle doit être utile, ce sera peut-être pour les calculs de la colinéarité (???)
à demain !
mais le vrai pb, c'est qu'il n'y a pas alignement (en tout cas, pas qq soit n!)
Je dirais plus : en déplaçant M sur
Donc j'aurais envie de dire que pour tout M sur
pareil pour moi, jeveuxbientaider.
(j'ai fait avec géogébra, M en point mobile, et je ne vois jamais alignement)
mais bon, je ne suis pas aussi calée que vous 
je me suis donc abstenue d'énoncer une certitude d'après une simple conjecture ^^
bizarre, quand mm, cette question :/ ... bref !
x1 = (x+7y+63)/50
bon cette fois-ci, je cut !
bonne nuit à tous 
C'est vrai qu'une figure sur Geogebra ne démontre rien ... elle permet juste de trouver des contrexemples pour prouver que la propriété à démontrer est fausse !
Je n'ai pas démontré ma conjecture mais elle me semble plus crédible que ce qui est demandé avec la transcription qu'on a eue de l'énoncé ! Est-ce vraiment l'énoncé complet ? ou une interprétation libre ? Personne ne nous le dira !
bonjour Labo;
oui, en effet c'est ce que l'on trouve en procédant par identification pour retrouver l'équation du cercle.
merci 
je suis désolé c'est un exo 1ère S qu'on m'a donné avec ces données
encore mea culpa je n'ai pas l'habitude de donner des énoncés bourrés de fautes.
Comment avez vous fait pour retrouver la bonne équation de cercle?
Bonjour,
parce que tu fais une erreur fondamentale de débutant : croire qu'avec un morceau de bout d'énoncé on peut résoudre une question isolée d'un exo.
c'est faux
les questions d'un exo sont liées et les définitions exactes de tous les points dans l'énoncé sont indispensables
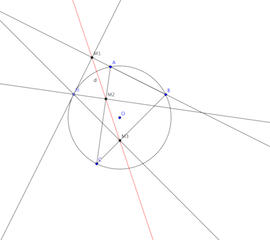
si je comprends bien (si je devine bien à travers ma boule de cristal) ton exo consiste à démontrer le théorème de Simson :
étant donné un triangle ABC et son cercle circonscrit 
soient M1 M2 M3 les projetés orthogonaux d'un point M sur les côtés du triangle (sur les droites)
alors M1 M2 M3 sont alignés si et seulement si M appartient à  sauf A, B et C eux même (parce qu'alors deux des points Mi sont confondus)
sauf A, B et C eux même (parce qu'alors deux des points Mi sont confondus)
RIEN dans ce que tu as écrit ici ne permet réellement de deviner ça...
et là bien entendu, avec cet énoncé corrigé ainsi, que ça va répondre à la question que M soit sur le cercle ou pas
M1 en fonction de x et y (M quelconque)
M2 et M3 idem
écrire la relation de colinéarité doit redonner ... l'équation du cercle !!
ce qui prouve le "si et seulement si"
(avec des coefficients qui disparaissent donc "valeurs interdites" si M en A, B ou C)
bonjour à tous
merci Mathafou, j'ai (encore) appris qqchose de nouveau 
Valparaiso,
te voilà rassuré, ça marche avec la bonne équation.
(d'après ce que je comprends de ta réponse, c'était écrit ainsi sur l'énoncé dont tu disposes?)
garde cette équation sous le coude, et focalise-toi d'abord sur la colinéarité des vecteurs M1M2 et M2M3, par ex.
Oui c'est ça carita!
Oui je vais calculer les coordonnées de ces 2 vecteurs et montrer qu'ils sont colinéaires.
Je posterai mes réponses.
Merci on arrive au bout!
un conseil :
quand tu auras les coord. du vecteur M1M2,
je te conseille de travailler la colinéarité à partir d'un vecteur u, colinéaire au vectM1M2,
donc tel que vectu =  vectM1M2
vectM1M2
en choisissant judicieusement  : les coordonnées de vect u seront plus "légères" pour les calculs à venir
: les coordonnées de vect u seront plus "légères" pour les calculs à venir
idem avec vectM2M3 :
cherche un vect v qui lui est colinéaire, et avec des coord. plus simples à manipuler
ah ok
j'ai calculé les coordonnées de M1M2 et si je les divise par 3/25 je trouve
(4x+3y+2;3x-4y-11)
est ce juste?
MERCI
OUI c'est ce que je fais
après avoir simplifié les coordonnées de M1M3 par 3/50
je trouve (13x-9y+19;-9x-13y+83)
et donc on devrait avoir
(4x+3y+2) . (-9x-13y+83)=(3x-4y-11) . (13x-9y+19)
et déjà les coefficients des x² : -36 et 39 ne correspondent pas
je désespère
perso, j'ai fait les calculs pour vectM2M3, plutôt que M1M3 (d'où ma préférence...)
et j'arrive à M2M3(x-3y+3 ; -3x-y+21) --- largement + sympa pour la suite 
le fait que les x² ne s'annulent pas est normal !
on sait que (cf message de Mathafou) on va arriver, en bout de calcul, à l'équation du cercle.
or dans l'équation du cercle, il y a du x²
donc pas d'affolement prématuré.
en revanche, je ne vais pas refaire les calculs sur M1M3
si tu es sûr de tes coord., poursuit ton calcul
ensuite pour poursuivre les calculs et montrer que les vecteurs sont colinéaires il faut montrer que xy'=x'y c'est bien cela?
avec M1M2(x;y)
M1M3(x';y')
oui, le coeff de x² et celui de y² (en revanche, ils doivent être égaux!)
s'ils ne sont pas =1,
divise les 2 membres de l'égalité par ce coeff commun
(pour les ramener à 1, donc)
puis compare ce que tu obtiens avec l'équation développée du cercle...
montre ton résultat si tu as un pb.
merci infiniment
je suis enfin arrivé à l'équation de cercle

laborieusement j'avoue mais j'ai pas fait S moi!!!