c'est juste mais je ne comprends pas bien tes calculs.
(surtout a²-4a+2=-2 de quel droit simplifies-tu les 2 ?)

quand tu as l'équation de la tangente y-(a²-3a+4)=(2a-3)(x-a)
et que tu veux qu'elle passe par E(2;-2) tu aurais dû remplacer x par 2 et y par -2 et écrire
-2-(a²-3a+4) = (2a-3)(2-a) développer, simplifier, etc ...
mais je ne retrouve pas ça dans ta ligne d'après -a²+3a-4=-2a²+7a-6 que je ne comprends pas bien. on dirait que tu as fait y=0 et x je ne sais pas trop quoi ?

Salut,

Pour la question 1, ta formule est bonne, mais puisque tu connais , il faut s'en servir pour calculer et , puis écrire l'équation de la tangente sous la forme (équation réduite), avec et à déterminer.

Bonsoir,

[Bonsoir tout le monde]

Je reconnais que ma présentation n'est pas très mathématique. Mais sur mon travail au brouillon j'ai mis que le tout était égal à -2 (valeur du y).
Je vais reprendre mes calculs avec une bonne présentation et je vais voir si au final je retrouve les mêmes équations.
En si peu de temps vous avez trouvez les solutions de cet exercice ?

Bonsoir Iderden,
je complète ma réponse 1 :

f(a) = a²-3a+4
f'(a) = 2a-3

y=(2a-3)(x-a)+a²-3a+4
y=2ax-a²-3x+4

et là je dois encore réduire la forme ?

Oui, tu écris

--> tu retrouves la forme (, comme tu veux), de l'équation réduite d'une droite dans un plan

Ensuite tu reprends le raisonnement de Glapion.

Merci beaucoup à tous !

Je termine demain !

Une équation de droite s'écrit sous la forme où représente le coefficient directeur de la droite, c'est à dire sa pente.

Une fonction est dérivable en    si      existe et est finie.

Si tel est le cas, alors la fonction    est dérivable en   et cette limite s'appelle nombre dérivé de     en et se note .

Il correspond à la pente de la tangente à la courbe de la fonction     en

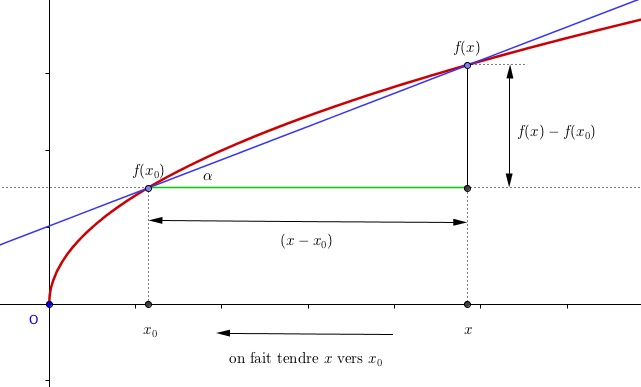
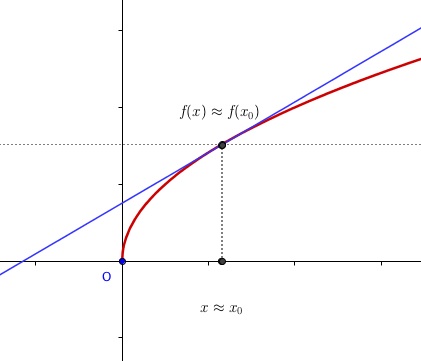
En faisant tendre vers la valeur , va aussi se rapprocher de , et la droite bleue va "se tangenter" à la courbe.

Ton , c'est en fait ta valeur limite de qui dans la première figure sera déterminer par :



c'est "la pente".

Donc, en un point de tangente, l'équation de la droite  (donc de la droite tangente à la courbe) sera sous cette forme :

Un autre approche un peu moins en "mode formule"

bien que ce soit au bout du compte la même chose, mais peut-être que celle-ci t'apportera une compréhension plus conséquente.

Soit le (ou les) point(s) de tangente recherché(s) et de coordonnées .
Soit la (ou les) tangente(s) à la courbe qui remplit (remplissent) les conditions suivantes : passer par le point (de tangente à la courbe)   et le point (extérieure à la courbe) .

est une tangente à la courbe, donc une droite, son équation s'écrit donc sous la forme :

où est le coefficient directeur de la droite tangente .



Les coordonnées de vérifient donc l'équation de la droite , nous avons donc :






Les coordonnées de vérifient donc l'équation de la droite , nous avons donc :




Or, est le coefficient directeur de la droite , laquelle tangente la courbe de au point , donc nous avons :



et comme



nous avons :



Ainsi, l'équation ci-dessus devient :



est un point de la courbe représentative de , ses coordonnées sont donc les suivantes :



ou encore dit autrement, nous avons :



L'équation devient donc :



d'où :



Il y a donc 2 points de tangentes vérifiant le fait que les dites tangentes passent aussi par le point , et leurs coordonnées sont donc :

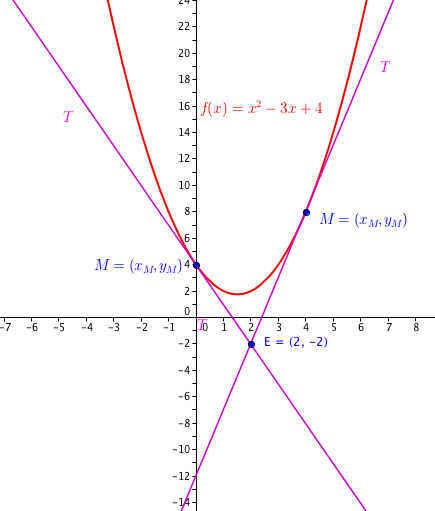
Merci beaucoup Jedoniezh pour cette réponse ultra complète. Je vais bien étudier ces deux variantes afin de bien comprendre mon travail.

Lis bien mon message de 07:42 pour bien saisir le fond de la notion.

Oui, c'est bien à ce message que je faisais référence !
Merci encore

De rien.

Et si tu as d'autres questions, n'hésites pas.

Un petit conseil, étudie la dérivabilité de la fonction au point