Inscription / Connexion Nouveau Sujet
Etude. d'une fonction
Bonjour à tous,
J'aurai besoin d'un peu d'aide concernant un exercice.
Je dois faire une étude complète de la fonction suivante : √((x-1)/(x+1))
Je suis bloqué à la partie dérivation. Pour la dérivée, j'ai trouvé 1/(√((x-1)/(x+1)) . (x+1)^2) mais cette dérivée n'admet pas de racine, du coup comment faire pour trouver les sommets ?
Merci d'avance pour vos réponses
bonjour
il me semble que la dérivée est juste 
et son signe est super facile à déterminer
signe de 1, signe du carré, signe de la racine.....
moi j'ai appris qu'une racine carrée était toujours positive ou nulle !! 
donc si tu prends bien les précautions d'ensemble de définition d'une part et de dérivabilité d'autre part avant de dériver, tout va bien !
Bonjour malou
Je reviens du jardin.
Je n'avais pas vu les parenthèses "extérieures" ((...)/(...))
Excuse moi zPersianBoy
Je trouve en faisant le tableau de la dérivée première qu'il n'y pas de sommets, pas de point d'inflexion, mais je trouve une tangente verticale en x=1 et x=-1, est-ce juste?
et du coup dois-je calculer la dérivée seconde?
Salut,
Pas tangente en -1, car f non définie.
Comment trouves-tu qu'elle n'a pas de point d'inflexion ?
dans quel but veux-tu chercher la dérivée seconde ?
En faisant le tableau de signe de la dérivée première, je trouve que( a part en -1 et 1) , la dérivée est positive et que la concavité ne change pas , ducoup je me dit que je devrais peut-être calculer la dérivée seconde
ducoup quand est-ce que je dois être sur qu'il faut utiliser la dérivée seconde?
quand on te le demande, quand on veut déterminer une concavité, quand on ne sait pas étudier le signe de la dérivée première....tout ça c'est fonction de l'exercice
Ca c'est assez douteux : E
n faisant le tableau de signe de la dérivée première, je trouve que( a part en -1 et 1) , la dérivée est positive et que la concavité ne change pas
Je te rappelle que la dérivée de x --> x3 est toujours positive, mais la concavité de cette fonction "change" ...
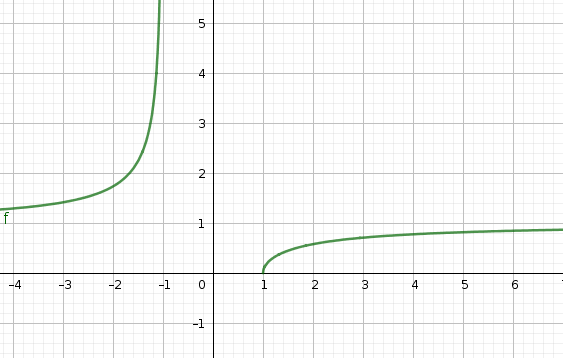
... et d'ailleurs sur le graphique, on voit clairement que la fonction étudiée est d'abord convexe, puis concave.
j'aurai juste une dernière question si cela ne vous dérange pas,
Lorsque je fait le tableau de signe de la dérivée première et que je veux montrer qu' au niveau d'un point où la fonction n'est pas dérivable, on a une tangente verticale, faut-il obligatoirement que la dérivée à gauche et la dérivée à droite de ce point soient toutes les deux infinies?
"La dérivée infinie" n'est pas correct, mais dans l'idée : une limite de f' "d'un seul côté" suffit.
"La dérivée infinie" n'est pas correct, mais dans l'idée : une limite de f' infinie "d'un seul côté" suffit.
faut-il obligatoirement que la dérivée à gauche et la dérivée à droite de ce point soient toutes les deux infinies?
non, pas du tout...
tu peux avoir une limite infinie d'un seul côté comme pour la fonction racine carré en 0