Bonjour,
Peux-tu préciser ce que tu entends par

Bonjour,
Bien sûr, il s'agit des fonctions du type :
Racine carrée de ( ax^2 +bx+c)

On vous en parle comme ça en première? Impressionnant!
Oui, a priori, une étude en fonction des valeurs (et donc du signe) de a, b et c.
Mais aussi les différentes formes:
Développée
Factorisée
Canonique

Donc sa fait beaucoup de cas à traiter ?

Ca dépend. En faisant l'étude, tu trouveras si les valeurs de a, b et c ont une importance ou pas.

Ok donc pour le domaine j'ai écrit qu'on a plusieurs cas

Cas 1 le delta (b^2 -4ac) est strictement plus grand que 0 : dans ce cas c'est le signe de a qui a de l'importance. Si a est positif, alors le domaine vaut <—;racine 1]U[racine2;—>
Et si a est négatif alors le domaine vaut : [racine 1;racine2]

Cas 2 si delta est nul le signe de a est important, si il est positif le domaine est R sinon si il est négatif le domaine est uniquement la racine

Cas 3 si delta est négatif. Si a est positif  alors le domaine est R sinon la fonction n'existe pas

Est-ce juste jusqu'à maintenant ?

Le "domaine", c'est le "domaine de definition"
On ne dit pas que la fonction n'existe pas, mais qu'elle n'est pas définie.

D'accord c'est noté mais à part ça est ce que ce que j'ai écrit est juste ?

Oui, mais le cas 2 avec a<0 n'a aucun intérêt.

Ok merci

Ensuite pour les racines , y'a t'il quelque chose de spécial à écrire? car moi je ne vois rien.

Non. Rien à part leur existence et valeur(s).

Ok

Et pour l'axe de symétrie si je mets qu'il est le même que pour le polynôme du second degré en dessous de la racine c'est bon ?

Oui.

Re bonjour à tous,

Pour la partie sur les tangentes horizontales et verticales et les sommets, j'ai trouvé que

Pour les tangentes horizontales, il faut calculer les points où la dérivée première s'annule ( sommet au sens de Fermat). Pour cela, j'ai trouvé une dérivée qui vaut (2ax+b)/(2.(√(ax^2+bx+c)) et qui s'annule en x= -b/2a. Est-ce juste?

Pour les tangentes verticales et les autres sommets, je ne vois pas comment je pourrais faire un tableau de signe.

Merci d'avance pour vos réponses

up, s'il vous plait

bonjour,

les 4 cas de figure intéressant à caractériser entièrement



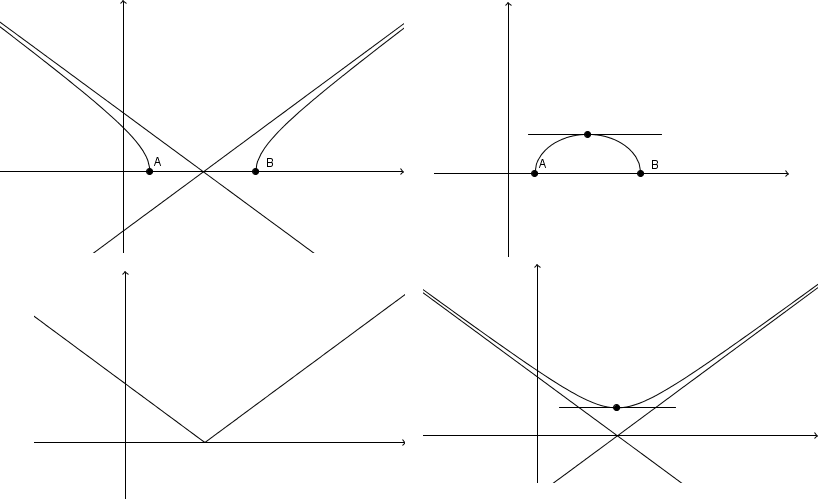
donc y compris les asymptotes obliques est il demandé
et les tangentes verticales (pas dessinées ici), c'est à dire les valeurs interdites de la dérivée en fait, pour lesquelles la dérivé devient "infinie".

il est inutile d'exprimer in extenso les valeurs des racines !! (on les appelle x1 et x2 et ça suffit)

on pourrait dire que si delta est >0, f(x) = racine(a(x-x1)(x-x2))
si delta <0, f(x) = racine(a((x-α)² + K)), K >0
et si delta = 0 hé hé
pour étudier "en détails" ces différents cas

Re bonjour,

J'aurais quelques questions par rapport à ce que vous avez écrit si ça ne vous dérange pas

Dans le schéma du 3 eme cas (en bas à gauche ) vous n'avez pas dessinez d'asymptote oblique, ça veut dire qu'il n' y en a pas ?

Ensuite je ne vois pas ce que le K signifie lorsque delta est plus petit que 0.

Merci d'avance

une droite est "asymptote" d'elle même
ce cas 3 correspond à l'ensemble de deux demi droites exactes !

K : si tu te réfères à la forme canonique d'une fonction du second degré
P(x) = a( x - α )² + β
on peut exprimer β en fonction de a et de Δ (cours)
mon "K" vient de là, en ayant mis a en facteur de sorte que (x-α )² + K soit toujours positif (et même ≥ K > 0) si &Delta est < 0 indépendamment du signe de a
de sorte que le signe de P(x) est le signe de a quel que soit x dans ce cas

ceci dit c'est juste une façon de voir les choses
on peut réciter le cours sur le signe de P(x) de différentes façons équivalentes, et rédiger ça de même.

Ok et pour le tableau de signe de la dérivée comment faire pour les différents cas ?

qu'est ce qui te bloque ?

  est du signe de la dérivée de u dans le domaine de définition ...

attention au cas Δ = 0 car u n'est pas ce qu'on croit mais est définie par morceaux (ou par une valeur absolue ce qui nous fait une belle jambe pour la dérivée, tiens)

Donc pour la dérivée je trouve : (2ax+b)/(2racine(ax^2+bx+c))

Lorsque delta est égal à 0 avec a positif, comment je justifie que la dérivée est définie par morceaux ?

Et pour les autres cas, je calcule les racines de la dérivée que j'ai trouvée Pour les tangentes horizontales et je fais un tableau de signe normal pour les tangentes verticales?

delta = 0 c'est la fonction elle même qui est définie par morceaux !!
parce que
c'est à dire +u si u est ≥ 0 et -u si u est <0


les racines de la dérivée ... hum
les racines de 2ax+b = 0 c'est vite vu !!

par contre les valeurs interdites pour la dérivées (donc les tangentes verticales), c'est par la nullité du dénominateur de la dérivée.

Re bonjour,

Excusez moi de vous déranger mais j'aurais quelques dernières petites question.

•Concernant le K, je ne comprends pas comment on met a en facteur à partir de la forme canonique?

•Pour la dérivée j'exprime le dénominateur de la dérivée en fonction des différentes écritures :  si delta est >0, f(x) = racine(a(x-x1)(x-x2))
si delta <0, f(x) = racine(a((x-α)² + K))?

Merci d'avance

a(x-α)² + β = a[(x-α)² + β/a] pardi, K = β/a
mais comme j'ai dit c'est juste une façon de voir

tu peux tout aussi bien dire que si Δ < 0 alors le trinome est du signe de a partout et c'est pareil.

"j'exprime le dénominateur de la dérivée"
tu cherches si il y a des valeurs de x qui annule ce dénominateur et c'est tout.
et si oui tu les appelles x1 et x2
et tu fais ça comme tu veux, que ce soit avec des écritures explicites (en fait on s'en fiche) ou juste en récitant le nombre de racines selon la valeur de Δ et point barre.

Parfait merci,
Ça pourrait paraître bête mais est-ce que l'ordre dans lequel je mets les valeurs qui annulent le dénominateur et le numérateur dans le tableau de signe a de l'importance ?

X1 et x2 sont n'importe laquelle des deux vu que tu n'en donneras pas la formule (surtout pas !!)


et on sait que si elles existent, l'abscisse de l'extrêmum du trinome ax² + bx + c est exactement (x1+x2)/2
(axe de symétrie d'une parabole)

donc dans un tableau ce sera (si présentes toutes les trois) "par convention"
-inf,   x1,   xM,   x2,   +inf

Parfait merci beaucoup à vous mathafou et sanantonio312 pour votre précieuse aide et votre temps 🙂

De rien.
C'est mathafou, que je salue au passage, qui a fait l'essentiel du boulot!