On considere la fonction f(x)= cos(x)+1/4cos(x)
1) Determiner le domaine de definition
2) Demontrer que le domaine d'etude peut etre reduit a un domaine d'amplitude pi et determiner ce domaine d'etude
3) Etudier les limites eventuelles de la fonction f pour son domaine d'etude
4) Calculer la derivee f'(x) et etudier son signe
5) Etablir le tableau de variation de f
6) Montrer que pour le point I (pi/2;0) est le centre de symetrie de la courbe Cf de la fonction f
7) Tracer soigneusement la courbe representative Cf de la fonction
8) Calculer la derivee f"(x) de la fonction f(x)
   a) Exprimer cette derivee en fonction de cos(x) seulement
   b) Determiner les valeurs de x qui annulent f"
   c) Quelles remarques peut-on tirer pour le graphique de Cf

Bon ca fait toute une journee que j'essaye de faire ce DM et je crois que c'est tout faux donc si quelqu'un pourrait bien m'aider ou ne serait-ce que m'expliquer un peu bon surtout a partir de etudier son signe a la 4) ca serait bien sympa parce que bon jusqu'a cette partie j'ai un peu pres mon idee mais bon pas sure du tout pour la 1) j'ai trouvee R* pour la 2) ]0;pi] pour la 3) j'ai pris les limites lorsque x tend vers pi et lorsque x tend vers 0 et jai trouvee -5/4 et 5/4 et finalement pour la 4) je trouve d'abord comme derivee f'(x) = -sin(x)-4sin(x)/16cos^2(x) et en simplifiant et factorisant le plus possible f'(x)=-sin(x)(1+1/4cos^2(x)
Ceux qui peuvent m'aider je les remercie deja enormement d'avance

Bonjour,

Le domaine de définition est -{/2+k; k} (si la fonction est bien définie par )
La fonction f n'a pas de limite, ni en + ni en -. Si l'intervalle d'étude est [0; ] (qui correspond à une demi période, l'autre demi période s'obtenant par symétrie axiale), la limite en 0 est f(0) et celle en est f()...
En revanche, puisque , la limite en /2 est infinie. Il faut distinguer la limite à gauche et celle à droite.

Venons-en aux questions qui te posent problème :
La dérivée est définie par     (car la dérivée de est )
Ce qui donne : , soit
En définitive, .

À partir de là, tu dois pouvoir continuer seul(e).

1)k appartient à Z et non à N
2) fest paire et periodique de periode 2pi donc dom d'etude est  
[0,pi/2[U]pi/2,pi]
3)lim cosx =0+ ==>limf(x)=+00
x-->pi/2         x-->pi/2
x<pi/2           x<pi/2
lim cosx =0-  ==> lim f(x)=-00
x-->pi/2          x-->pi/2
x>pi/2           x>pi/2

4) on ta donne la derivee
5)sur [0,pi]  :  sinx>0 et (2cosx)² >0donc le signe de f' est celui de
(1+2cosx)(1-2cosx)

6) il suffit de montrer que f(pi -x)+f(x)=0

7)a)je revient à  f'(x)=-sinx  +(sinx)/4cos²x
f"(x)=-cosx +[(cosx)(4cos²x)-(4cos²x)'(sinx)]/(16cos^4 (x) )
      =-cosx  +[4(cosx)^3  + 8(sinx)²(cosx)]/(16(cosx)^4 )
     =[-16(cosx)^5  +4(cosx)^3 +8(1-cos²x)(cosx)]/(16(cosx)^4 )
     =[(4cosx)(-4(cosx)^4 -cos²x +2]/(16(cosx)^4 )
     =[-4(cosx)^4 -cos²x +2]/(4(cosx)^3 )

f"(x)=0 <==> -4(cosx)^4 -cos²x +2=o
on pose X= cos²x  avec  0<X<1
sauf erreure

bonjour, je ne comprends tout de meme toujours pas a la 4) comment on etudie le signe de cette derivee avec les zeros de f'et a la 5) pour le tableau de variation la seule chose que je sais c'est que sur le domaine d'etude [0;pi] cette fonction est decroissante mais comment l'expliquer et comment placer les zeros def'(x) dans ce tableau ? sans avoir dresse le tableau correctement je ne pourrais pas tracer pour la 7) une courbe correcte. Finalement pour la 3) avec l'etude des limites pourquoi etudier seulement celle de pi/2 et non celle de 0 et pi qui sont les bornes de cette fonction ?

bon pour les 0 de f j'ai trouvee tout d'abord x=0, x=pi/2, x=2pi/3 j'imagine que comme pi est une borne et pi/2 une valeur interdite il y a quelquechose a etudier avec leur signe et quelquechose a preciser dans le tableau de variation je suis presque sure mais j'ai aucune idee de comment m'y prendre

dans un exo fait en classe du meme style ou f(x)=x^5/5(1-5/3*1/x^2) et sa derivee etait x^4-x^2=x^2(x-1)(x+1)
le prof de maths avait fait l'etude de signe de la sorte
comme x^2 > ou = 0 sur Df, le signe de f' est celui de (x-1)(x+1)
pour x E ]-oo;-1[ f'>0 donc f croissant
pour x = -1 f'=0 en changeant de signe avec f maximum
pour x E ]-1;0[ f'<0 donc f decroissant
pour x=0 f'=0 sans changer de signe donc f inflexion
pour x E ]0;1[ f'<0 donc f decroissant
pour x=1 f'=0 en changeant de signe avec f minimum
pour x E ]1;+oo[ f'>0 donc f croissant

j'essaye d'appliquer quelquechose du meme style pour cette etude de signe mais j'y arrive vraiment pas ... aidez moi s'il vous plait
merci davance

svp aidez moi sa m'enerve de pas trouver et pourtant je  cherche ...

Bonjour,

Pour la question 4, je repars de la dérivée que je t'ai donnée plus haut :
.

Il suffit d'étudier le signe de chacun des facteurs sur l'intervalle d'étude [0; ] :

le facteur (sin x) est positif pour tout x dans cet intervalle. Il s'annule pour 0 et pour .
le facteur (1-2 cos x) s'annule pour x=/3, est positif avant et négatif après cette valeur,
le facteur (1+2 cos x) s'annule pour x=2/3, est négatif à gauche, puis positif à droite,
le terme qui est au dénominateur est positif car c'est un carré. Il s'annule pour x=/2 (là où la fonction n'est pas définie...)
Avec tout ça, tu peux faire un tableau de signe (sans oublier la valeur "interdite" /2) et voir que la dérivée est successivement :
- négative sur [0;/3]
- positive sur [/3;/2[ puis sur ]/2;2/3]
- négative sur [2/3;]

Naturellement le tableau de variation n'est plus ensuite qu'une formalité.

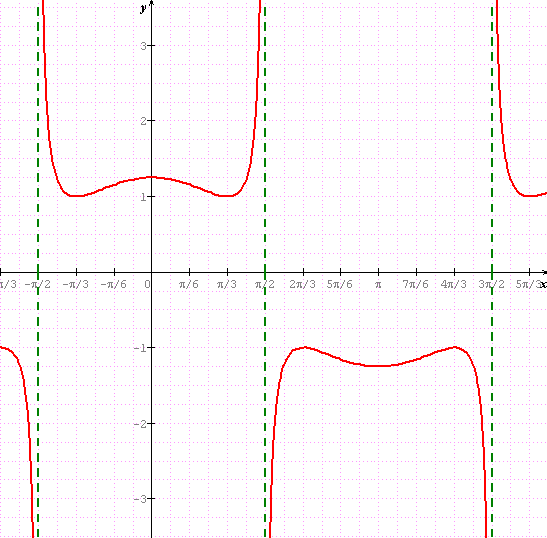
Voici un aperçu de la courbe sur l'intervalle [0; ]] :

vous vous etes trompes pour la derivee vous avez oubliez de mettre le sin(x) en facteur

Exact, je me suis trompé, mais le signe étudié est correct : j'ai bien tenu compte du facteur (sin x) (c'est même le premier facteur étudié). C'est simplement un oubli au moment de taper la dérivée... Tout le reste est correct.

merci beaucoup l'aide m'a ete vraiment utile par contre je ne suis pas tou a fait d'accord avec la courbe. en tapant la derivee a la calculatrice elle me montre une courbe sinusoide comme celle de la fonction cosinus ou sinus ou tout simplement comme la fonction de depar de l'exerice

Bonjour,

La courbe que j'ai dessinée est celle de la fonction f définie par :, sur [0;].

Si tu obtiens une sinusoïde avec ta machine, c'est tout simplement que tu as oublié de mettre des parenthèses autour de (4 cos x) car alors, la fonction que tu dessines est définie par :
c'est à dire :
ce qui n'est pas du tout la même chose !

merci beaucoup pour m'avoir explique. On fait tellement d'erreurs d'etourderie en maths que c'est parfois difficile d'avancer dans un exercice, l'exercice lorsqu'il est donc etudie par une autre personne est d'une aide incroyable parce l'approche est faite dans dans un different point de vue. Merci donc enormement pour votre aide en esperant que si j'ai encore des questions vous serez toujours a l'ecoute.  

quelqu'un pourait-il m'expliquer si on etudie les limites de pi et 0 aussi et pa seulement de pi/2 pour la 3) et aussi pour la 6) comment on peut montrer que I est centre de symetrie ?
merci davance

bonjour julie


6) Montrer que pour le point I (pi/2;0) est le centre de symetrie de la courbe Cf de la fonction f


il te faut montrer que, pour tout x tel que pi/2+x et pi/2-x appartenant au Df, :

f(pi/2+x)+f(pi/2-x)=2f(pi/2)=0

A toi de jouer...

Philoux

merci enormement et pour les limites alors ? les autres n'ont que pris en compte pi/2 alors que moi j'ai calculee celle de pi et 0 puisque ceux sont les bornes du domaine d'etude est-ce correct pour la 3) ou la limite de pi/2 suffit ?

en fait ta fonction est définie en x=0 et x=pi

on ne parle donc pas de limite...

Je te joins la courbe

bon courage: je quitte l'île

Joyeux Noël !

Philoux

Bonjour,

Comment fait-on pour obtenir une image sinequanon sans déformation ? Je ne suis pas très au fait des différents formats d'images, mais, personnellement, je copie l'image dans paint et je l'enregistre au format GIF avant de la joindre à mon message... Le résultat n'est pas très bon.
L'image sinequanon native est au format wmf (dans le presse papier) mais je ne sais pas comment la joindre à un message du forum...

Merci de m'éclairer

merci enormement philoux, patrice rabiller sans oublier drioui
Joyeux noel et bonne annee