Inscription / Connexion Nouveau Sujet
Etude d'une fonction non dérivable en un point de son ensemble d
(Re)Bonsoir, il s'avère que je bloque sur tous mes exos ^^' alors... en voila un autre. Merci à vous d'avance 
On considère la fonction f définie sur ℝ\{2} par f(x)= (3x−9)/(x−2).
1. Dresser le tableau des variations de la fonction f.
Déjà fait.
2. Résoudre l'équation f(x) = 0 et en déduire le signe de f(x) sur ℝ\{2}.
Déjà fait.
3. Déterminer l'équation réduite de la tangente à la courbe de f au point d'abscisse 3.
4. Représenter graphiquement avec amour et soin, la courbe de la fonction f dans un repère
orthonormal du plan (utiliser du papier millimétré).
5. Soit 
la fonction définie sur ℝ\{2} par (x)=∣f(x)∣ .
a) A partir de la représentation graphique de f , en déduire celle de .
b) La fonction est-elle dérivable en 3 ? Justifier la réponse.
c) Donner l'expression algébrique explicite de (x) sur ℝ \ {2}.
d) En se plaçant successivement sur les intervalles ]2 ; 3[ et ]3 ;+∞[ , étudier la dérivabilité de la
fonction en 3.
e) La fonction est-elle dérivable en 3 ? Justifier la réponse.
bonsoir,
3) la tangente a pour equation réduite:
y = f'(3)(x-3)+f(3)
il suffit de calculer f'(3) et f(3) et de remplacer.
4- voici la courbe de f en bleue et celle de en rouge
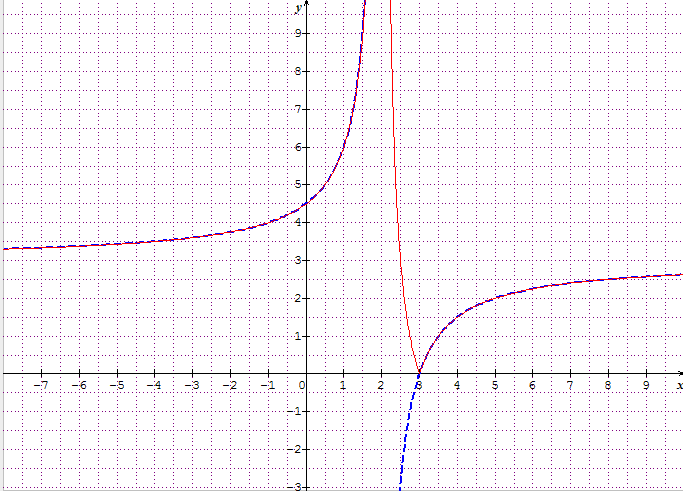
5- a)la courbe de ets identique à celle de f quand f(x) ets positif.
Le morceau tel que f(x) est negatif doit etre symétrisé par rapport à l'axe de x pour avoir la courbe de
b) regarde ce qui se passe au point (3;0) : il y a un point de rebroussement de la courbe, la tangente à droite est differente de la tangente à gauche, donc la fonction n'ets pas dérivable.
c) pour x 
3 f(x) = (x−9)/(x−2).
pour x
3 f(x) = (9-3x)/(x-2)
d) là tu etudies la limite de [f(3+h)-f(3)]/h pour h qui tend vers 0+ puis vers 0-
e) tu as dû trouver deux valeurs différentes à la question d) donc la fonction n'est pas derivable en 3.
Merci beaucoup, par contre, pourrais tu m'expliquer pourquoi à la question 5-c) tu prends x3 et x3 ainsi que le calcul de l'expression s'il te plait.
parce que j'ai ecrit une bêtise!
J'ai repondu trop vite excuse moi...
en fait (x) = f(x) quand f(x) est positif.
et quand f(x) est negatif, (x) = -f(x)
donc pour x 
]-
;2[ 
[3;+[ (x) = f(x) = (x−9)/(x−2).
pour x]2;3], (x) = -f(x) = (9-3x)/(x-2)
oki? 
Annuler
connectez vous