Inscription / Connexion Nouveau Sujet
Etude de la fonction cube
Bonjour,
J'aimerai avoir de l'aide sur un exercice sur la fonction cube.
Voilà l'exercice:
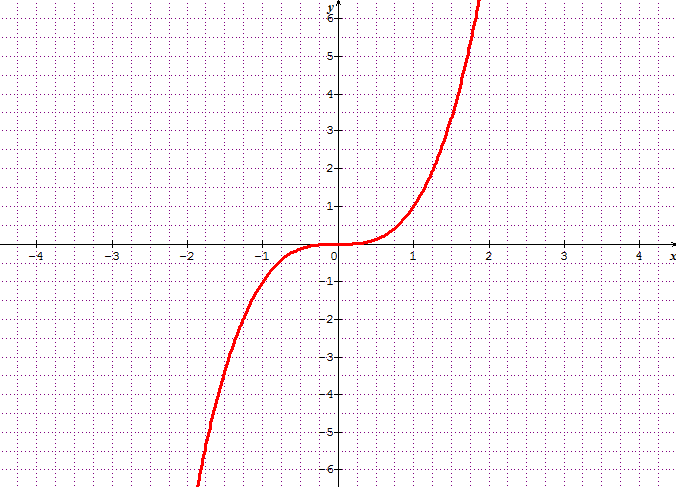
"Soit g la fonction définie sur R par g(x) = x3 et C sa courbe représentative dans le repère orthonormal (O I J).
1. Tracer soigneusement la courbez de la fonction cube sur une feuille de papier millimétrée.
2. Quelle conjecture peut-on formuler concernant le sens de variation de la fonction cube?
3.a
Vérifier que si a et b sont deux réels, alors g(a)-g(b)= (a-b)((a+)2+
).
b
En déduire le sens de variation de la fonction g.
4.
Justifier que C admet un centre de symétrie.
Merci,
J'ai du mal surtout pour la question 3a et 4
pour la 3.a on te demande simplement de vérifier, donc tu n'as qu'à développer l'expression donner et vérifier que çà te donne bien g(a)-g(b).
Pour la 4. intéresse toi à la parité de la fonction 
Annuler
connectez vous