Inscription / Connexion Nouveau Sujet
Etude du signe d'une fonction rationnelle
Bonjour voici une partie de mon DM.
Soit f définie sur ]5,+ [ par:
[ par:
F(x)=3x-2
x²+3x-10
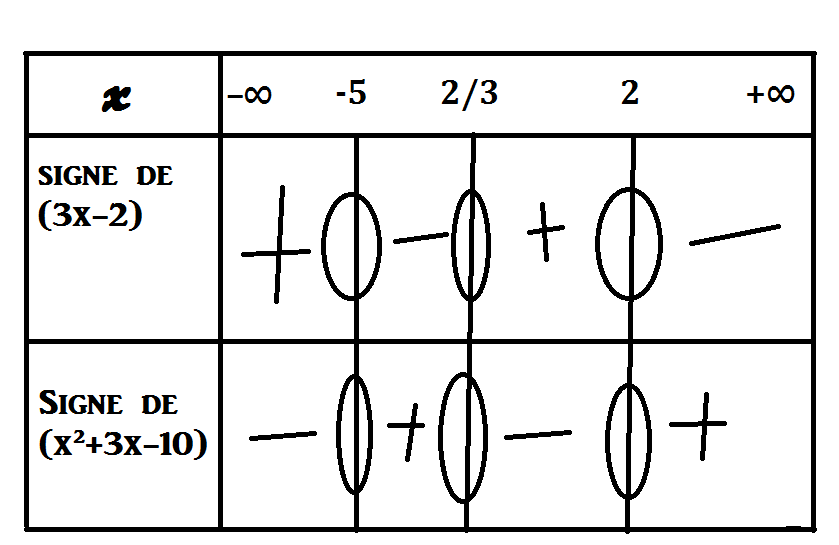
1. Etudier dans un tableau le signe de f(x) lorsque x varie dans ]5,+ [
[
2. Resoudre dans ]5,+ [ l'inéquation f(x)
[ l'inéquation f(x) 0
0
Merci de pouvoir m'aider et a toute 
Etude du signe de f(x):
Calcul des racines:
f(x)=0 (3x-2)/(x²+3x-10)=0
(3x-2)/(x²+3x-10)=0
 3x-2=0 ou x²+3x-10=0
3x-2=0 ou x²+3x-10=0
 3x=2 ou x²+3x=10
3x=2 ou x²+3x=10
 x=2/3 ou x²+......
x=2/3 ou x²+......
je trouve sa mais ensuite je bloque sur le 3x car je ne sais pas quoi faire du x si je fait divisé par 3.
pouvez vous m'aider a compléter ceci? 
si ce n'est pas le cas, d'après le domaine de définition tu peux dire de quel signe est l'expression x²+3x-10.
tu as dû voir les propriété des fonctions du second degré.
La forme canonique te permet de connaitre le sommet de la parabole et le signe du coefficient du second degré te donne les variations de la fonction par rapport au sommet
il faut que j'utilise  ?? c'est pas normal vu que je doit résoudre les deux parties ? si ?et oui il me semble que oui
?? c'est pas normal vu que je doit résoudre les deux parties ? si ?et oui il me semble que oui
en fait ce qui me bloque c'est que
x²+3x=10 (sa ok)
x²+x=10/3 (sa ok)
mais apres que faire du x en trop ?? la est mon problème  je sais pas si vous voyez ce que je veut dire
je sais pas si vous voyez ce que je veut dire 
sa donne x x+x mais que se passe t'il sur cet exercice ?
x+x mais que se passe t'il sur cet exercice ?
Tu parles de  .
.
Donc tu as vu les équations du second degré.
il faut chercher les racines du polynome.
x²+3x-10
je trouve ceci:
Cette fois on a :
k=-10
Il faut donc trouver 2 nombres dont le produit est égal à -10
Il y a 2 solutions :
-10=(-2)x5
-10=2x(-5)
ce que j'écrirai désormais sous la forme :
-10=( 2)x(
2)x( 5)
5)
Mais on sait que la somme des deux racines vaut -b, c'est à dire -3
On en déduit que les racines sont 2 et -5
il manque le signe de f(x).
D'autre part on ne met 0 que sur les valeurs qui annulent l'expression.
ex: pour 3x-2, inutile de mettre 0 sur -5 et 2 ce qui engendre des erreurs. D'ailleurs le tableau est incorrect.
Si tu factorises le dénominateur, c'est pour faire apparaitre l'expression factorisées ton tableau.

 s'il vous plaît merci
s'il vous plaît merci