Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. PremièreForum de première [tout]Lister tous les topics de mathématiques
Niveau première
Partager :

Exercice 1 DM

Posté par
Lowlow93 15-09-10 à 13:04

Bonjour j'ai un exercice a faire pour demain et je n'arrive toujours pas à le faire sauf que maintenant le temps presse je n'ai plus beaucoup de temps, j'ai besoin de votre aide s'il vout plait! Merci beaucoup d'avance !

Exercice 1 DM

** énoncé effacé ; image laissée **

Edit Coll : si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum     

Posté par
Lowlow93Exercice 1 DM 15-09-10 à 13:10

Je ne demande pas de me donner la réponse, juste m'aider pour la démarche merci

Posté par
Eric1re : Exercice 1 DM 15-09-10 à 13:11

Bonjour

Appelle x la longueur AM par exemple, et trouve l'aire des deux jardins en fonction de x

Posté par
pppare : Exercice 1 DM 15-09-10 à 13:53

Bonjour à tous
exercice intéressant, pr lequel je peux te proposer mes pistes.

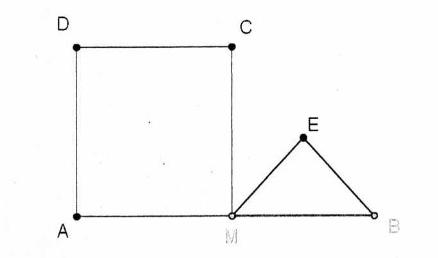
A la différence de Eric, j'ai posé MB = x.

L'aire du jardin est dc composée de la somme de l'aire du carré AMCD et de celle du trg rtg en E et isocèle EMB.

Aire du carré : facile : (4-x)²

Aire du trg EMB : moins évident mais pas insurmontable pr un/e élève de 1ère.

C'est tjs : (Base * Hauteur) / 2

Soit  : [MB] la base choisie, et H la projection orthogonale de E sur [MB]
la hauteur relative à la base [MB] est dc EH, et comme EMB est un trg isocèle de sommet principal E (le sommet principal d'un trg isocèle, c'est celui dt partent les 2 côtés égaux), H est le milieu de [MB].
Par ailleurs, du fait que EMB est un trg isocèle de sommet principal E, (EH) est aussi la bissectrice intérieure de l'angle 3$\widehat{MEB}, qui mesure 90 °.

EMH est dc un trg rtg en H, avec 3$\widehat{MEH}=\widehat{EMH}=45\rm dgr

L'aire du trg cherchée sera dc 3$\frac{EH.MB}{2}=\frac{EH.x}{2}

reste à trouver EH.

On sait que ds le trg rtg en H EMH, 3$\frac{EH}{EM}=\sin 45\rm dgr =\frac{\sqrt{2}}{2}, mais comme on connait pas EM, il faut déterminer EM.

Tjs ds le trg EMH, 3$\frac{MH}{EM}=\frac{\frac{x}{2}}{EM}=\sin 45\rm dgr =\frac{\sqrt{2}}{2}.

Dc 3$x=\sqrt{2}.EM, soit 3$EM=\frac{x.\sqrt{2}}{2}

Tjs ds le trg EMH, 3$\frac{EH}{EM}=\cos 45\rm dgr =\frac{\sqrt{2}}{2}.

Dc 3$EH=\frac{\sqrt{2}.EM}{2}=\frac{x}{2} après simplifications.

Dc l'aire du trg EMB est : 3$\frac{MB.EH}{2}=\frac{x.\frac{x}{2}}{2}=\frac{x^2}{4}.

Soit f l'aire des jardins en fonction de x . On a 3$f(x)=(4-x)^2+\frac{x^2}{4}=\frac{5x^2}{4}-8x+16.

cette fonction qui représente l'aire est à valeur minimale pr la valeur de la variable x qui annule sa dérivée première.

On a dc l'aire minimale des 2 jardins le long du mur de 4 m selon les formes souhaitées pr 3$f'(x)=\frac{5}{2}x-8=0, soit 3$x=\frac{16}{5}=3.2

Le carré aurait dc 80 cm de côté.

Voilà, j'espère que tu comprendras et que tu sauras refaire.

Si tu as des questions, j'y répondrai ce soir.

Posté par
pppare : Exercice 1 DM 15-09-10 à 13:54

Oui, l'énoncé était pas très long, t'aurais pu le recopier..

Posté par
Eric1re : Exercice 1 DM 15-09-10 à 13:56

Effectivement, c'est un peu plus simple à écrire avec x=MB

Posté par
pppare : Exercice 1 DM 15-09-10 à 17:47

>>Eric

ma 1ère idée était aussi de poser AM = x, mais qd je me suis (assez vite) aperçu  que c'est surtt l'aire du trg qui serait la - facile à déterminer, j'ai interverti la nomination des distances sur [AB]

Posté par
pppare : Exercice 1 DM 15-09-10 à 17:50

>>Lowlow

Citation :
cette fonction qui représente l'aire est à valeur minimale pr la valeur de la variable x qui annule sa dérivée première.


Pr être + précis, qui annule la dérivée première et la fait changer de signe, ce qui est bien le cas ici

Posté par
Eric1re : Exercice 1 DM 15-09-10 à 17:50

J'y ait pensé juste après avoir posté, mais je me suis dit que ça l'aurait embrouillé de changer... surtout si je n'étais pas allé jusqu'au bout

Posté par
pppare : Exercice 1 DM 15-09-10 à 22:07

Finalement je me rends cpte qu'on peut déterminer EH sans avoir à déterminer EM, en posant direct : 3$\frac{MH}{EH}=\frac{\frac{x}{2}}{EH}=\tan 45\rm dgr = 1 \rm d'ou EH=\frac{x}{2}.

Bcp + rapide --> inutile de reprendre les calculs pr déterminer EM, et confirmation que la valeur de EH en fonction de x est la bonne.


Rechercher
Menu
Espace membre
25 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1725 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !