Inscription / Connexion Nouveau Sujet
Exercice 1ereS
Bonjour quelqu'un pourrai-ilt résoudre ce problème avec, s'il vous plait, une partie rédaction complète mentionnant la réponse:
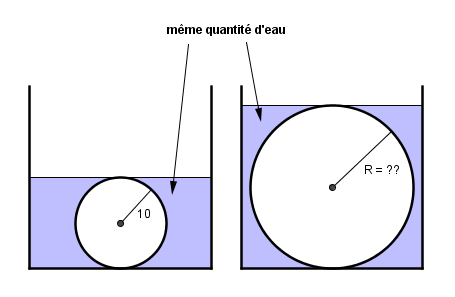
On considère un récipient cylindrique de rayon intérieur 20cm et de hauteur 44cm
On place une boule de rayon 10cm plus dense que l'eau au fond du récipient puis on verse de l'eau jusqu'à recouvrir exactement la boule
on enlève cette boule et on la remplace par une seconde boule de meme densité et de rayon r(pas égale a 10 cm)
la question est
Est il possible que l'eau recouvre exactement la deuxieme boule?
Merci d'avance de votre réponse.
J'ai regardé mais c'est pas exactement la même question donc j'aimerais bien que l'on m'aide pour celle ci
bonjour,
On place une boule de rayon 10cm plus dense que l'eau au fond du récipient puis on verse de l'eau jusqu'à recouvrir exactement la boule
calcule le volume d'eau
volume de la boule : (4/3)pi * 103
on verse de l'eau jusqu'à recouvrir exactement la boule :
volume cylindre :
hauteur 20 cm Aire base = 20²pi -> v=203pi
volume d'eau : 203pi- (4/3)pi * 103=......................
on enlève cette boule et on la remplace par une seconde boule de meme densité et de rayon r(pas égale a 10 cm)
mêmes calculs , sauf que r est la mesure du rayon de la bille. (on remplace 10 par r)
A toi
Bonjour,
citation de quelqu'un qui a répondu sur un autre forum où Loutouful a posé sa question :
Il y a des gens qui passent du temps à inventer des exercices qui permettent aux étudiants de progresser. Il y a des étudiants qui passent du temps à demander des solutions toute faite pour... ne pas pouvoir progresser ?
Donne-nous plutôt des idées, les difficultés que tu rencontres etc.
j'adore ...
certes, réponse peu constructive, mais pourtant ... il doit y avoir un fond de vérité là dessous.
J'ai regardé mais c'est pas exactement la même question
tu n'as surement pas dû regarder attentivement parce que si, c'est la même question tout au moins dans un bon paquet du nombre considérable de discussions sur le même sujet.
regarder attentivement des sujets semblables, même si ce n'est pas exactement la même question, permet d'avoir des idées de recherches et de calculs à effectuer.
la figure que j'ai dans mes archives est comme par hasard avec le rayon du récipient = 10
coïncidence, ou c'est justement parce que ce problème a déja été exactement traité ?
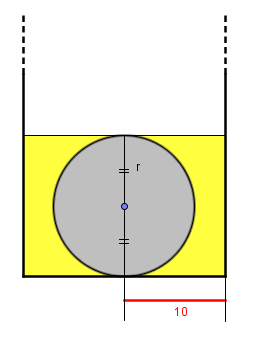
faire le bilan des volumes comme dit kenavo27
volume d'eau = constante = volume du cylindre "eau+bille" moins volume de la bille
non
ce terme en rouge est faux :
203pi- (4/3)pi * 103 = 203pi - (4/3)pi*R3
tu n'as pas remplacé partout le rayon initial de 10 cm par "R" dans le cas de la bille de rayon R
quand on change de bille la hauteur totale de l'eau varie : elle est toujours 2R, c'est la condition pour que la surface affleure au sommet de la bille, quel que soit son rayon inconnu R.
en plus tu avais une parenthèse fermante en trop (pas de parenthèse ouvrante correspondante, mais bon, faute de frappe)