Inscription / Connexion Nouveau Sujet
Exercice 4
Bonjour !
Je voudrais rendre un maximum de devoirs sauf que je bloque sur un exercice qui m'empêche de l'envoyer..
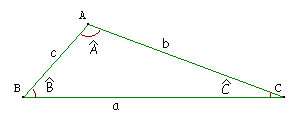
(Les informations sont sur l'image)
voici les questions :
1. Dans le triangle ABE, quelle est la relation correcte permettant de calculer la mesure de l'angle ABE :
a) AB^2=AE^2+BE^2-2AB.BE.coABE
b) AE^2=AB^2+BE^2-2.AB.BE.cosABE
c) BE^2=AB^2+AB^2-2.AB.BE.cosABE
2. Quelle est la valeur de BE^2
3. Quelle est la valeur de AE^2
4. En déduire la valeur de cos ABE
5.En déduire la valeur de l'angle ABE
Merci d'avance.
** image recadrée sur la seule figure, tout le reste est interdit en image **
Bonjour,
Je vois que tu es nouveau, bienvenue sur l'
Ton image a été recadrée conformément à ![]() Sujet ancien- ne plus donner ce lien-merci (Clique sur ce lien).
Sujet ancien- ne plus donner ce lien-merci (Clique sur ce lien).
Prends le temps de lire ce sujet et complète ta demande en répondant à ton propre message et en respectant désormais les règles du site.
Quelqu'un va te venir en aide quand tu l'auras fait
- recopie de l'énoncé, photos et scans de textes interdits,
- ce que tu as essayé, commencé, fait, ce qui te bloque précisément
Oupsi, pardon j'avais mal présenté mon sujet😅
Enfin bref, donc les longueurs du carré à pour longueurs 1.
J'ai répondu à la première question (1) et j'ai répondu le petit a.
Cependant, je ne sais pas quelle formule appliquée pour répondre à la question n°2 et n°3..je ne comprends pas.. je peux donc pas répondre à la n°4 et n°5..
Merci pour votre aide.
Rebonjour,
il manque des infos
ce qui est dans l'énoncé en plus de ce que tu as raconté
recopier c'est mot à mot, pas en "oubliant" les données définissant les différents points par exemple.
c'est bien écrit explicitement dans ![]() Sujet ancien- ne plus donner ce lien-merci
Sujet ancien- ne plus donner ce lien-merci
mais l'as tu vraiment lu ce lien, obligatoire ?
on ne raconte pas, on recopie mot à mot.
Voici l'énoncé, en entier..:
L'exercice qui suit est un exercice comportant trois parties. Chacune des parties peut être traitée de façon indépendante.
ABCD est un carré de côté 1
Les points E et F sont tels que vecteurCE= 3/2vecteurCD et vecteurBF = 3/2vecteurBC
Dans la première partie, on s'intéresse à un algorithme codé sous python.(déjà fait)
L'objectif dans la seconde partie est de montrer que les droites (AF) et (BE) sont perpendiculaires (déjà fait), et sans la troisième partie on cherche à déterminer la mesure d'un angle sur cette figure (c'est donc cette partie sur laquelle je bloque..)
On considère le repère orthonormé (B; vecteurBC; vecteurBA)
Ah.. oui là je ne suis vraiment plus..
Je ne comprends pas..
Et le théorème de pythagore, tout simplement ?
Et pardon, je ne sais pas mettre la flèche pour les vecteurs au dessus des deux points..
PS: question1 réponse a) , c'est faux
dommage que tu l'aies précisé, mathafou : j'aurais aimé que Zigozhas se rende compte de son erreur à l'issue de son calcul.
Zigozhas,
tu peux utiliser pythagore, pourquoi pas ? ou te placer dans le repère pour calculer les distances..
si tu as plusieurs outils pour calculer une distance, tu choisis celui que tu veux.
je ne vois pas pourquoi tu dis "Ah.. oui là je ne suis vraiment plus.. Je ne comprends pas.. " qu'est ce que tu ne comprends pas ?
Je ne comprends justement pas la question 1.. je suis au cned et ce chapitre j'ai beaucoup de mal. Donc je ne comprends pas comment fonctionne cette relation..
Sinon, d'accord merci beaucoup. Le théorème de Pythagore, je suis au point donc je vais choisir cette option. Enfaite, je me demandais pour Pythagore car avec les relations du dessus, je croyais que ça allé être plus complexe on va dire
je quitte : je reviens voir ce soir si tu as terminé (à moins que mathafou reste là...)
A tout à l'heure.
et "je ne sais pas mettre la flèche pour les vecteurs"
écrire "vecteur" comme le fait Zigozhas suffira.
sur ce je vous laisse poursuivre.
l'image doit t'aider pour la question 1.
si tu écris cos A, le premier terme de l'égalité est le coté opposé à l'angle ( a² dans mon exemple).
Ah d'accord ! Merci beaucoup donc pour la question 1 c'est le petit b) car le côté qui est opposé à (B^) c'est le côté AE.
Par contre, qu'est-ce qu'ils demandent en disant "la valeur de cos(B^m" ? Je reprends justement la relation de la question 1 et j'applique mes valeurs dans celle-ci ? Car maintenant je connais justement les valeurs de AE^2 et BE^2
Okay.
Et donc j'ai remplacé :
AE^2=AB^2+BE^2-2.AB.BE.cos(B^)
1,11=1+1,80-2.1.1,80.cos(B^)
Pour BE, j'ai utilisé Pythagore.
concentre toi, BE² n'est pas égal à 1,80
de plus, garde des valeurs exactes, ce sera plus juste.
BE² = ????
AE² = ???
non, je te dis que tes valeurs sont fausses.
AE ² = ???
AE est l'hypoténuse du triangle AED rectangle en D.
BE² = ??
BE est l'hypoténuse du triangle BCE rectangle en C.
allez vas y !
Par contre j'ai un temps de retard dans vos réponses.. je fais ce que vous dites et être étourdi arrive..
Par contre j'ai un temps de retard dans vos réponses.. je fais ce que vous dites et être étourdi arrive..
oui, oui, je sais
 ca n'est pas grave, on se comprend.
ca n'est pas grave, on se comprend. Alors pour BE^2 :
J'ai fais
AE^2=AB^2+BE^2
= 1^2+0,5^2
AE = racine carré de 1,25 = Racine carré de 5/2
AE^2=AB^2+BE^2 ??? dans quel triangle rectangle te places tu ?
AE ² = 5/4 = 1,25 OK
BE² = BC² + CE²
BE² = 1² + (3/2)² = 13/4
BE = ( 13) /2
13) /2
....
Ah oui.. dans le triangle ADE !
Et pour ce qui est de BE^2 pour Pythagore je me place dans le triangle BCE !
Et d'accord, merci. Je ne sais pas si je serai présente plus tard..
Un énorme merci si jamais je ne peux pas revenir..
Bonne soirée.
au cas où je suis toujours là ...
Holala...
quand on s'aperçoit d'une erreur dans ce qu'on a écrit il vaut mieux tout réécrire le bon calcul en entier plutôt que d'en corriger un petit bout isolément, puis un autre car alors on ne sait plus vraiment quel est le bon calcul ni ce qu'il représente ...
oui, pour appliquer Pythagore , il faut se placer dans un triangle rectangle.
les formules de la question 1 fonctionnent dans tous les triangles, y compris dans les triangles rectangles.
finalement,
en plaçant dans la formule b) les valeurs exactes que tu connais, tu as pu écrire
cos ABE = ??
et en utilisant ta calculatrice (avec arccos), tu trouves un angle de quelle mesure ?
Bonsoir,
Pardon je suis partie.
Du coup, donc je prend ma relation et je remplace toutes les valeurs que je connais mais le cos(B^) je ne le marque sur la calculatrice ? Si ?
Je marque bien :
AE^2=AB^2+BE^2-2.AB.BE.cos(A^)
Soit :
2,5=1+13-2×1×(racine carré de 13/2).cos(A^)
...
C'est le .cos(A^).. je ne sais pas ou le mettre..
C'est comme une équation en soit ? Je mets mon 2,5 à droite ? Ou je n'y suis pas du tout ?^^'
c'est pas cos A, c'est cos B (cos ABE)
oui "C'est comme une équation"
c'est même exactement une équation, en l'inconnue "cosB"
l'inconnue ne s'appelle pas toujours "x"
ça peut très bien être être c, t, y, XA, ...,cos(B) etc etc
AE² n'est pas égal à 2,5, BE² n'est pas égal à 13 etc .
AE ² = 5/4 = 1,25 OK
BE² = BC² + CE²
BE² = 1² + (3/2)² = 13/4
BE = (
 13) /2
13) /2
....
Donc si je rectifie mes valeurs cela donnerai :
Cos(B^)=1+13/4-2×1×(racine carré de 13/2-1,25
...
Mes valeurs sont bonnes ici ?..
non.
tu traites ton équation de façon incorrecte
c'est comme si tu avais, par exemple
7 = 4 + 9 - 5x
que ferais tu ?
certainement pas
x = 4 + 9 - 5 -7 !!
tu commencerais par 5x = 4 + 9 -7
et en simplifiant tout ce qu'on peut simplifier :
5x = 6 car 4 + 9 -7 ça fait 6
puis x = 6/5 (on divise les deux membres par 5)
ici c'est le même principe.
Ah oui d'accord ! Oui je vois, non pour l'exemple que vous m'avez donné, je n'aurais pas fais comme avec l'équation que je suis entrain de résoudre. Je mets de côté mon "2xABxBE", je ne le mets pas avec mon cos(B^)
Donc ça ferait :
2x1x(Racine carré de 13/2).cos(B^2)= -1,25+1+(13/4)
... ?