Inscription / Connexion Nouveau Sujet
Exercice
Bonsoir à tous .
J'aimerais que vous m'aidez à faire cet exercice . Merci d'avance .
Soit ABC un triangle ,B' et C' les milieux respectifs des côtés [AC] et [AB]. On désigne par D le symétrique de A par rapport à B , E le symétrique de C par rapport à A et F le milieu de [DE].
Démontrer , en utilisant le théorème des barycentres partiels , que F ,B' et C' sont alignés . Préciser leurs positions relatives.
Voici ce que j'ai commencé à faire
<=> C'=bar {(A,-3);(D,4)}
Or -
<=>A=bar{(C,-1);(E,-1)}
Donc C'=bar{(C,-1);(E,-1);(D,4)}
CB' = 4CE ??
Tu pourrais commencer par écrire que C' est barycentre de A et B, puis définir les points A et B comme barycentres d'autres points.
C'=bar {(A,1);(B,1)}<=> C'= bar {(A,2);(B,2)}
A=bar {(C,1);(E,1)} et B=bar {(A,1);(D,1)}
C'=bar {(C,1);(E,1);(A,1);(D,1)}
Or B'=bar {(A,1);(C,1)} <=>
C'=bar {(B',2);(E,1);(D,1)}
On a aussi F milieu de de [ED] d'où F =bar {(E,1);(D,1)}
D'où C =bar {(B'2);(F,2)}
<=> C est le milieu de [B'F] .
Merci à vous .
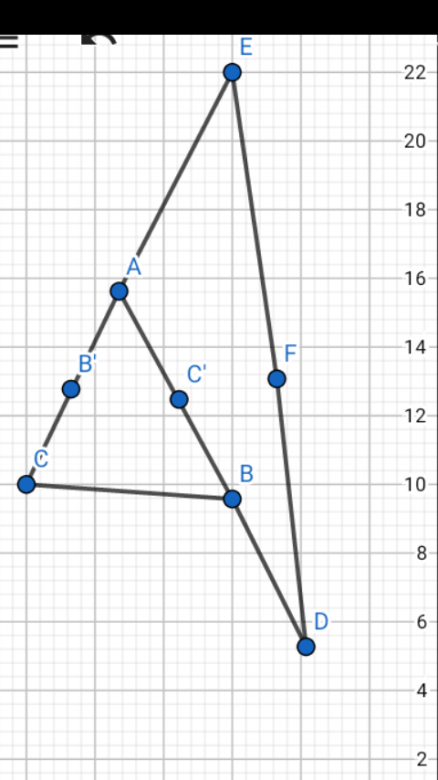
Je pense qu'il faut commencer par un dessin plus précis.
On dit que D est le symétrique de A par rapport à B.
Donc B devrait être au milieu entre A et D.
Dans ton dessin, ce n'est pas le cas, B est quand même plus proche de D que de A.
Tu as un 'papier' quadrillé. Compte les carreaux pour positionner D correctement.
Ce sera plus facile si tu places A B et C sur les sommets des carreaux, et pas au milieu d'un carreau.
Pour la résolution de l'exercice, ça ne changera pas grand chose. Mais c'est la partie la plus facile de l'exercice, autant la faire bien.