Inscription / Connexion Nouveau Sujet
Exercice angle orienté
Bonjour à tous, j'ai un exercice de math sur les angles orientés qui me pose quelques soucis, si quelqu'un pouvait me donner un coup de main c'est gentil. Par contre je ne peux pas mettre la figure alors je vais tenter de vous expliquer :
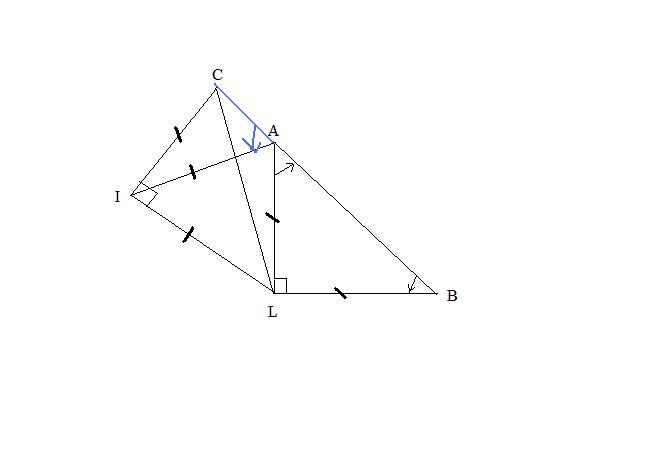
Dans la figure, AIL est un triangle équilatéral (au milieu de la figure), ALB est un triangle rectangle isocele en L ( donc collé à AIL)(donc à droite), et ICL est un troisieme triangle, qui est rectangle isocele en I (à gauche).
1/ Donner la mesure principale de l'angle oritenté (
;
) ayant pour mesure (175
)/8
J'ai réussi et j'ai trouvé -/8
2/ a. Quelle est la mesure de l'angle géométrique IAC , en déduire une mesure de (vecteurAI;vecteurAC)
(j'ai besoin de votre aide, j'ai beaucoup de mal avec les angles orientés! )
b. Calculer (vecteurAB;vecteurAC), que peut on en déduire pour les points A,B,C
(on voit bien qu'ils sont alignés, mais je n'arrive pas )
Merci de votre aide ! Bonne soirée
Bonjour,
on a AI=IL=IC donc AIC est un triangle isocèle en I. On peut trouver et ensuite la valeur des autres angles mais j'ai besoin de plus de précisions.
Pour l'orientation, par convention, on oriente le plan dans le sens trigonométrique (c'est-à-dire dans le sens inverse des aiguilles d'une montre).
Peux-tu essayer de reproduire la figure sous paint ou scanner et transformer le scan en format png ou autre pour pouvoir l'insérer ?
Le triangle ALB est rectangle et isocèle en L. Donc AL = LB et l'angle ALB = /2
Propriété : Dans un triangle isocèle les angles LAB = LBA. Dans ce cas chaque angle vaut /4 (car la somme des angles d'un triangle est . Dans triangle ALB, on a /2 + /4 + /4 = , le compte y est).
Le Triangle AIL est équilatérale, c'est-à-dire chaque angle vaut 60° ou /3. Donc les angles AIL = ILA = LAI = /3.
a)Pour trouver l'angle IAC, d'abord il faut trouver l'angle AIC. C'est facile, car l'angle LIC est droit c'est-à-dire /2 et l'angle LIA = /3.
Donc l'angle AIC = /2 - /3 = /6
Maintenant qu'on a trouvé l'angle AIC, on peut calculer l'angle IAC. Etant donné que le triangle AIC est isocèle en I (IC = IA = IL), la somme des angles IAC + ACI = - /6 = 5/6
C'est-à-dire que l'angle IAC est égale à la moitié de 5/6
L'angle IAC = 5/12.
b) Pour calculer (vecteur AB, vecteur AC), c'est-à-dire l'angle entre les deux demi droite [AB) et [AC), il faut additionner tous les angles qui sont dans ce coin,
L'angle CAB = l'angle CAI + l'angle IAL + l'angle LAB = 5/12 + /3 + /4 = 12/12 =
Donc l'angle CAB est un angle plat, par conséquent les points A, B, C sont alignés
Annuler
connectez vous