Inscription / Connexion Nouveau Sujet
Exercice angle orienté
Bonjour, j'aurai besoin d'aide pour un exercice sur les angles orientés.
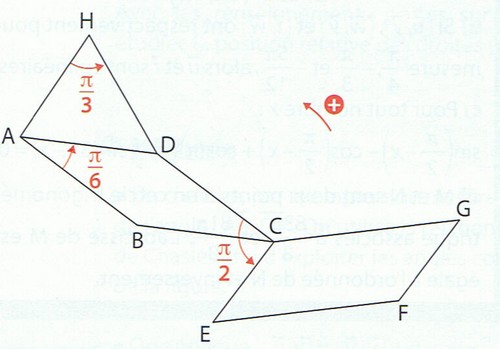
Dans le plan orienté, on considère la figure ci-dessous où ABCD et CEFG sont deux parallélogrammes tels que (AB,AD)=
/6 et (CD,CE)=/2. AHD est un triangle équilatéral tel que (HA,HD)=/3.
Objectif : Montrer que les droites (AH) et (FG) sont parallèles.
1. Décomposer l'angle de vecteurs (AH,FG) en utilisant la relation de Chasles et les vecteurs AD et AB.
2. Démontrer que (AB,FG)= /2
3. Conclure
Je bloque à la premiere question, j'ai plusieurs solutions mais ça n'utilise pas AD et AB. Pouvez-vous m'aider ?
Merci d'avance
bonjour,
1) La relation de Chasles te permet d'écrire :
(AH,FG) = (AH, AD) + (AD,AB) + (AB,FG)
2) (AB,FG) ?
en vecteur : AB = DC et FG = EC
donc (AB,FG) = (DC, EC)
ret tu sais que (DC,CE) = pi/2 ...
tu sais terminer ?
Merci Leile, mais pour la question 1, il faut mettre directement (AB,FG) ? Ou il faut d'abord écrire toutes les étapes car sans justification, ce n'est pas si évident, non ?
J'ai plus ou moins compris la suite, je vais le refaire correctement pour être sûre ! Mais après nan je ne pense pas savoir le faire... Je crois qu'il faut que la somme des angles fasse 2. Est-ce bien ca ?
Annuler
connectez vous