Inscription / Connexion Nouveau Sujet
Exercice avec Pythagore
Bonjour, voilà j'ai reçu cette exercice à faire mais je n'y arrive pas vraiment et je suis pas très bon en math, je recherche du soutient.
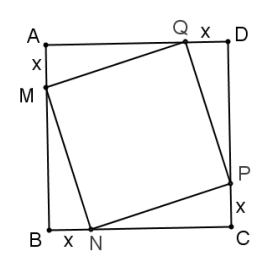
ABCD est un carré de côté 7 cm.
On construit le carré MNPQ, comme indique sur
la figure, avec :
AM = BN = CP = DQ = x et x appartient [0;7]
Déterminer le minimum de l'aire du carré MNPQ
Donc sur cet exercice, le prof nous a dit d'utiliser Pythagore, mais je ne sais pas trop comment m'en servir ici. Puisque si x=0, les deux carrés seraient identiques et donc l'aire serait de 7² soit 49 cm². Mais je ne pense pas que sa soit la bonne réponse ...
Bonsoir,
on te demande l'aire minimum de MNPQ, pas son aire maximum 
"avec Pythagore" tu calcules le côte MN "en fonction de x"
cela te permet de calculer l'aire de MNPQ "en fonction de x"
et en étudiant cette fonction aire(MNPQ) = f(x), en trouver le minimum.
Ah oui l'aire minimum oups ...
Donc
MN² = BM² + BN²
MN² = (7-x)² + x²
MN =  (7-x)² + x²
(7-x)² + x²
Et après il faut que je fasse un tableau de variation sur [0;7] ?
c'est pas MN l'aire ...
donc tu étudies la fonction Aire = f(x) = MN² = (7-x)² + x²
(tableau de variations, ou cours sur le trinôme du second degré...)
Donc f(x) = MN² = (7-x)² + x²
Si j'utilise f(x), je peux trouver l'aire minimum grâce à mon cour sur le trinôme du second degré ?
bein oui ! quoi d'autre ? c'est ce que j'ai écrit !
cours sur le trinome (résultats du cours directs), ou méthode pour étudier des trucs du second degré (forme canonique etc) vue en cours ...
il faut bien entendu commencer par développer et simplifier f(x) ...
Ok, merci de ton aide, je te ferais part de mon résultat demain pour voir si il est bon en attendant je vais me coucher. Bonne nuit et encore merci !
Désolé de déterrer un sujet d'il y a 4 ans mais serait -il possible d'avoir + d'explications car j'ai le même exercice à faire et je n'y comprends rien .