Inscription / Connexion Nouveau Sujet
exercice comprenant des systèmes
Bonjour
je bloque sur une question de mon exercice
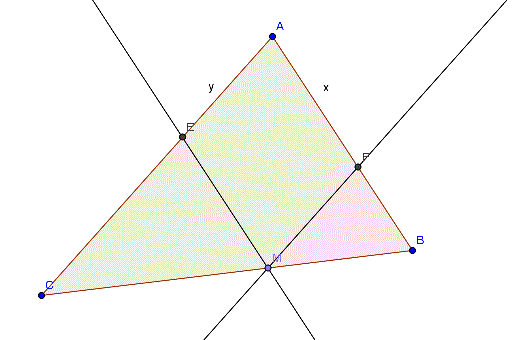
Voici le sujet: On considère un triangle ABC tel que AB=15 et AC=17. On prend un point M sur le segment [BC] et on construit les parallèles à (AB) et (AC) passant par M. La première coupe (AC) en E. La deuxième coupe (AB) en F.
mais avant je devais calculer deux systémes
Est-ce que quelqu'un sait comment je pourrais répondre à cette question : " Quelle est la position du point M si p=32 ? "
j'ai fait la figure,j'ai démontré que c'était un losange et j'en est conclu que le périmètre d'un losange était p=2(c1+c2)
donc j'ai calculé le périmètre pour trouver p=32
et maintenant comment puis-je faire pour donner la position de M ?
merci d'avance !
d'accord,
voilà :
Résoudre les systèmes d'équations:
a {17x+15y b{17x+15y=255
y=-x+16,5 x+y=15,5
On considère un triangle ABC tel que AB=15 et AC=17. On prend un point M sur le segment [BC] et on construit les parallèles à (AB) et (AC) passant par M. La première coupe (AC) en E. La deuxième coupe (AB) en F.
ON obtient le parallélogramme(éventuellement plat)AEMF.on note:AF=x et AE=y
2a. faire une figure
b)montrer que : 17x+15y=255
c)AEMF peut-il être un losange?
3Calculer les logueurs des côtés du parallélogramme AEMF lorsque son périmètre p vaut 33
4)Quelle est la position du point M si p=32
et la je blogue pour la 4
as-tu résolu les systèmes ?...le 1er est incomplet....
pour le 2-b) utilise le théorème de Thalès dans le triangle ACB coupé par la droite (ME) parallèle à (AB)
3) si le périmètre du parallélogramme vaut 33 alors tu as
2(x + y) = 33 donc x + y = 16,5
il te faut donc résoudre un système pour trouver x et y
Bonjour,
4)Es tu d'accord pour dire que : ?
Connaissant p tu peux connaître x et y (cf question 3) et donc connaître la position de M grâce à cette égalité vectorielle.
Sauf erreur bien entendu 
oui j'ai résolu les système
mais pour le 2b) lorsque j'ai remplacé les droites par les donnéesje trouve 17x sur 15y mais je ne trouve pas le 255
Pouvez-vous m'expliquer Tilk_11 s'il vous plait
Je veux bien laisser Tilk t'expliquer, mais notons le fait que 17*15=255 ... Y a peut être une histoire d'aire la dessous.
oh je ne voulias pas vous vexer Noflah c'est juste qu'il a commencé à m'expliqué mais merci de m'avoir répondu c'était tout bête je n'y ai même paa pensé ! :S mais vous pouvez continué à m'aidé ça me rendrai service ! 
oh je ne voulias pas vous vexer Noflah
Tu ne me vexes pas du tout, j'aime bien expliquer ce que je comprend bien, je suis sûr d'être dans les meilleur dispositions pour aider l'autre à comprendre. Mais expliquer quelque chose que je ne comprend pas tout à fait, je ne m'y risque point. C'est pour ça que sur ce point, manœuvre de sécurité, je laisse la parole à tilk

Bonjour à vous tous,
Tilk_11
[...]
2(x + y) = 33 donc x + y = 16,5
il te faut donc résoudre un système pour trouver x et y
Bonsoir, je m'étais absenté...
Pour la question 2-b) dans le triangle ACB, puisque (ME)//(AB), le théorème de Thalès te donne :
donc
...(EM=AF=x car AFME est un parallélogramme)
soit
...(les produits en croix sont égaux)
et en développant
Bonsoir Tilk_11
Ne t'inquiète pas pour mon intervention... Elle n'était que de passage.
Mais comme il fait calme sur l' , j'avais envie de me dégourdir les doigts sur le clavier.
, j'avais envie de me dégourdir les doigts sur le clavier. 
Je te laisse te dégourdir les tiens ! 
Bonjour Hiphigenie 
eh oui, c'est presque calme plat sur l' ...
...
rassure toi, ton intervention sur l' est toujours bienvenue
est toujours bienvenue 
Bonjour,
Un peu de hors sujet ... Où est-ce que vous trouvez le smiley de l'île ? L'autre jour je le voulais et je l'ai pas trouvé ...
Ici ![]() [lien]
[lien]
En bas de la page, sur "Smileys", tu cliques sur "liste complète des smileys" 
non je n'y arrive pas !
que veule dire les  avant le AB et après le AC
avant le AB et après le AC
je ne comprend pas coupquoi il y a 2 AB et 2 AC
Bonjour,
les ...//... signifient : "...est parallèle à...."
ainsi
(ME)//(AB) signifie "la droite (ME) est parallèle à la droite (AB)"
je ne comprend pas coupquoi il y a 2 AB et 2 AC
de quelle question s'agit-il ?
peux-tu être plus précis ?
Connaissant p tu peux connaître x et y (cf question 3) et donc connaître la position de M grâce à cette égalité vectorielle.
Sauf erreur bien entendu[quote]
je ne compra son égalité vectorielle
désigne la norme du vecteur
c'est à dire sa "longueur"
pour l'égalité vectorielle, Noflah utilise des notions que, à ma connaissance, l'on n'a pas encore en 1ère
un vecteur ne peut être égal à un nombre....
Pour trouver la position de M, il te suffit de connaitre la valeur de x et celle de y
on te dit que p =32 dans ce cas tu as 2(x + y)= 32 donc x + y =16
et comme tu as démontré que 17x + 15y = 255
il te suffit de résoudre le système
connaissant x et y tu pourras placer le point M
il me semble que c'est la façon la plus simple de procéder
Bonjour,
Si je peux me permettre mathildamivi, j'ai bien préciser dans mon message que comme à la question 3, connaître p te permet de trouver x et y. Seulement Tilk, je trouve un peu léger de dire "une fois que l'on a x et y on connait M". C'est bien le cas, mais grâce à l'égalité vectorielle que je donne, sinon connaître x et y ne donne pas la position exacte de M à mon sens.
Après je ne connais pas bien le programme de 1ere mais les vecteurs c'est bien au programme non ?
>Noflah
dans l'énoncé il est bien précisé que M est situé sur [BC] de cela il résulte que E est sur [AC] et F est sur [AB], donc connaissant x on peut placer E sur [AB] et de là placer le point M sur [BC] (la connaissance de x implique celle de y...)
Oui je suis d'accord que géométriquement on peut placer M, moi je parlais analytiquement. Enfin peu importe. Faudra bien s'y mettre. Tant que mathildamivi a compris je ne dis rien.
Bonjour tout le monde ! 
j'ai egalement cet exercice a faire et j'aimerais savoir ce que mathildamivi avait trouvee pour la premiere question avant de verifier mes resultats.
J'aimerais egalement savoir comment faire la question 2)c) soit AEMF peut-il etre un losange et j'ai du mal pour la fin de cet exercice...
Je vous remercie d'avance de jeter un oeil sur mes questions !

Bonjour Zbib 
va faire un tour ici---->![]() exercice niveau seconde tiré du manuel bordas
exercice niveau seconde tiré du manuel bordas
Un grand merci ! 
j'apprecie vraiment l'aide que vous donnez à tous les éleves qui ont des difficultés à faire des exercices en maths comme moi... 
Le topyc date un peu mais comme je fais ce devoir aussi en ce moment j'ai réfléchit un peu et j'ai trouvé plus simple.
si p=32 alors x + y = 16
en cherchant x on trouve : AF = x=7.5
en cherchant y on trouve : AE = y = 8.5
De plus, on connait les longueur de AB et AC, qui sont respectivement : 15 cm et 17 cm
On constate donc que x se trouve au milieu de AB et y au milieu de AC.
AF // EM
AE // FM
Donc, là, en utilisant le theoreme des milieu (vu en 4eme et 3eme) qui est :
"dans un triangle, si une droite passe par le milieu d'un coté et est parallèle au deuxieme coté alors elle pass epar le milieu du troisieme coté"
C'est plus simple,non ? 



