Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. PremièreForum de première Fonctions polynômeTopics traitant de fonctions polynôme [tout]Lister tous les topics de mathématiques
Niveau première
Partager :

Exercice de 1ere S - Fonction pôlynome.

Posté par
Likedream 25-09-15 à 19:20

Bonjour / Bonsoir !
J'ai des difficultés sur un exercice, dont voici l'énoncé :

f est la fonction polynôme de degré 2 définie sur R par f(x)=-2x²+24x-40. P est sa courbe représentative dans un repère. A et B sont les points d'intersection de la parabole P avec l'axe des absicisses et M est un point de P dont l'abscisse a est comprise entre les abscisses de A et de B. On note S(a) l'aire du triangle ABM.

1) Déterminer la position du point M pour laquelle l'aire de S(a) est maximale.
2) déterminer les positions du point M pour lesquelles S(a) 100. Arrondir au centième.

Pour la question 1 j'ai déterminé A et B en calculant ce qui m'a donné A(2;0) et B(10;0).
Je pense que  quand la fonction atteint son maximum l'aire du triangle est elle aussi maximale mais je ne suis sûre de rien.

Pour la question 2 : Je me doute qu'il faut faire une inéquation qui reprend "Base * Hauteur / 2 " mais je ne sais pas comment calculer la hauteur.

Si quelqu'un pouvait m'aider ce serait gentil
Merci

Posté par
GreenTre : Exercice de 1ere S - Fonction pôlynome. 25-09-15 à 19:28

Bonjour ;

Citation :
Je pense que  quand la fonction atteint son maximum l'aire du triangle est elle aussi maximale mais je ne suis sûre de rien

Citation :
Pour la question 2 : Je me doute qu'il faut faire une inéquation qui reprend "Base * Hauteur / 2 " mais je ne sais pas comment calculer la hauteur.


En prenant comme hauteur , celle issue du point M , et donc [AB] comme base , on voit bien que la hauteur = l'ordonnée de M. Avec ça , tu peux faire les 2 questions.

Posté par
Likedreamre : Exercice de 1ere S - Fonction pôlynome. 25-09-15 à 19:34

Citation :
En prenant comme hauteur , celle issue du point M , et donc [AB] comme base , on voit bien que la hauteur = l'ordonnée de M. Avec ça , tu peux faire les 2 questions.


Je comprends, donc l'inéquation serait 8xh/2 100 ?

Posté par
GreenTre : Exercice de 1ere S - Fonction pôlynome. 25-09-15 à 19:37

Oui. Tu peux expliciter h en l'exprimant en fonction de a.

Posté par
Likedreamre : Exercice de 1ere S - Fonction pôlynome. 25-09-15 à 19:44

Je vois mal comment l'exprimer en fonction de a, h correspond à l'ordonnée de M c'est correct aussi non?

Posté par
GreenTre : Exercice de 1ere S - Fonction pôlynome. 25-09-15 à 19:57

Tu ne peux pas résoudre l'inéquation si tu n'exprimes pas la hauteur en fonction de a, car l'inéquation porte sur a.

h est l'ordonnée de M. Et l'ordonnée de M est ...

Posté par
Likedreamre : Exercice de 1ere S - Fonction pôlynome. 25-09-15 à 20:00

L'ordonnée de M est 32
:?

Posté par
Likedreamre : Exercice de 1ere S - Fonction pôlynome. 25-09-15 à 20:02

Sachant que a = 8

h = 32 / 8 ?  

Posté par
GreenTre : Exercice de 1ere S - Fonction pôlynome. 25-09-15 à 20:04

Non. Tu vois bien que l'ordonnée de M dépend de a. M est d'abscisse a , et se situe sur la courbe P , donc..

Posté par
Likedreamre : Exercice de 1ere S - Fonction pôlynome. 25-09-15 à 20:13

Donc a ne représente pas la "distance" entre A et B.
M est l'image de a par la fonction f donc en calculant l'antécédent de a je trouve l'ordonnée de y ?

Posté par
GreenTre : Exercice de 1ere S - Fonction pôlynome. 25-09-15 à 20:19

J'ai l'impression que tu te mélanges les pinceaux là. a est défini comme l'abscisse du point M. M étant sur la courbe P , l'ordonnée de M est tout simplement l'image de a par f , donc c'est f(a).

Posté par
Likedreamre : Exercice de 1ere S - Fonction pôlynome. 25-09-15 à 20:24

Ah oui tout simplement x)


Merci beaucoup de ton aide en tout cas, passe une bonne soirée !

Posté par
Jedoniezhre : Exercice de 1ere S - Fonction pôlynome. 26-09-15 à 07:52

Bonjour à tous,

Ne nous privons pas d'une image.

1) Déterminer la position du point M pour laquelle l'aire de S(a) est maximale.

f a pour expression :

f(x)=-2x^2+24x-40,

donc de la forme :

f(x)=\underbrace{a}_{a<0}x^2+bx+c\text{ où }a=-2<0

On sait donc que cette parabolle sera "tournée vers le haut" (car le coefficient du x2 est négatif,

donc l'extremum de la courbe sera un maximum (=sommet de la parabole, si a coefficient de x2 avait été positif, la courbe aurait eu un minimum).

A partir du moment où l'on a dit cela, on sait que l'aire du triangle ABM sera :

Aire_{ABM}=\frac{1}{2}\times AB\times IM=\frac{1}{2}(x_B-x_A)(y_M-y_I)=\frac{1}{2}(10-8)(f(a)-0)=\underbrace{\frac{1}{2}(10-8)}_{\text{=valeur constante}}\times \underbrace{f(a)}_{\text{=vameur variable}}

A partir de cette expression, on voit bien que la variation de l'aire du triangle ne dépend que de la valeur variable, à savoir l'ordonnée du point M, c'est à dire f(a).

Donc si f(a) est maximum, l'aire sera maximum.

Donc l'aire sera maximum pour M au sommet de la dite parabole.

CQFD

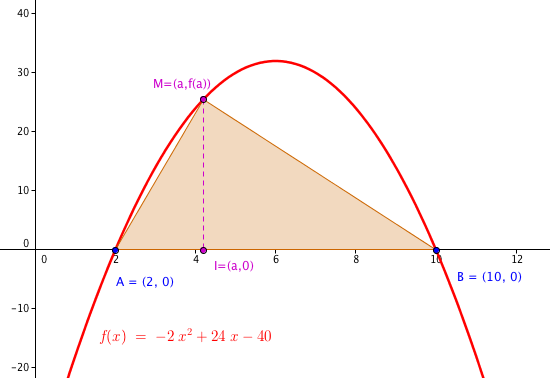
Exercice de 1ere S - Fonction pôlynome.

Posté par
Jedoniezhre : Exercice de 1ere S - Fonction pôlynome. 26-09-15 à 07:56

Je reprends, en supprimant faute d'orthographe et faute de frappe.

Bonjour à tous,

Ne nous privons pas d'une image.

1) Déterminer la position du point M pour laquelle l'aire de S(a) est maximale.

f a pour expression :

f(x)=-2x^2+24x-40,

donc de la forme :

f(x)=\underbrace{a}_{a<0}x^2+bx+c\text{ où }a=-2<0

On sait donc que cette parabole sera "tournée vers le haut" (car le coefficient du x2 est négatif,

donc l'extremum de la courbe sera un maximum (=sommet de la parabole, si a coefficient de x2 avait été positif, la courbe aurait eu un minimum).

A partir du moment où l'on a dit cela, on sait que l'aire du triangle ABM sera :

Aire_{ABM}=\frac{1}{2}\times AB\times IM=\frac{1}{2}(x_B-x_A)(y_M-y_I)=\frac{1}{2}(10-8)(f(a)-0)=\underbrace{\frac{1}{2}(10-2)}_{\text{=valeur constante}}\times \underbrace{f(a)}_{\text{=vameur variable}}

A partir de cette expression, on voit bien que la variation de l'aire du triangle ne dépend que de la valeur variable, à savoir l'ordonnée du point M, c'est à dire f(a).

Donc si f(a) est maximum, l'aire sera maximum.

Donc l'aire sera maximum pour M au sommet de la dite parabole.

CQFD

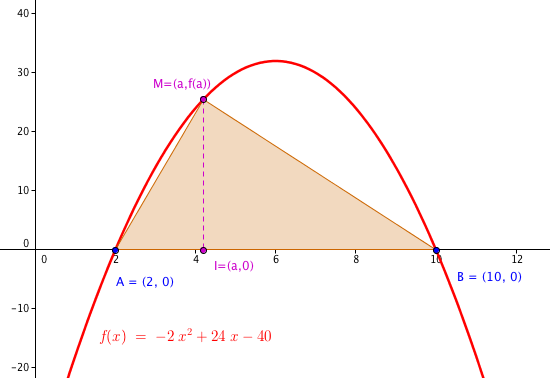
Exercice de 1ere S - Fonction pôlynome.

Posté par
Jedoniezhre : Exercice de 1ere S - Fonction pôlynome. 26-09-15 à 08:17

Désolé, j'ai laissé ci-dessus une faute de frappe, le développement de l'expression est :

Aire_{ABM}=\frac{1}{2}\times AB\times IM=\frac{1}{2}(x_B-x_A)(y_M-y_I)=\frac{1}{2}(10-2)(f(a)-0)=\underbrace{\frac{1}{2}(10-2)}_{\text{=valeur constante}}\times \underbrace{f(a)}_{\text{=vameur variable}}

2) déterminer les positions du point M pour lesquelles S(a) 100. Arrondir au centième.

A partir de l'expression ci-dessus, on obtient :

Aire_{ABM}=\frac{1}{2}(10-2)\times f(a)=4f(a)

Donc on a :

S(a)=Aire_{ABM}\geq 100\Longleftrightarrow 4f(a)\geq 100\Longleftrightarrow f(a)\geq 25

Donc, les valeurs recherchées seront les abscisses des points d'intersection (sur la figure C et D) de la courbe de f avec la droite d'équation y=25.

Les positions du point M telles que S(a)\geq 0 correspondent donc à :

x_M=a\in[x_D,x_D]

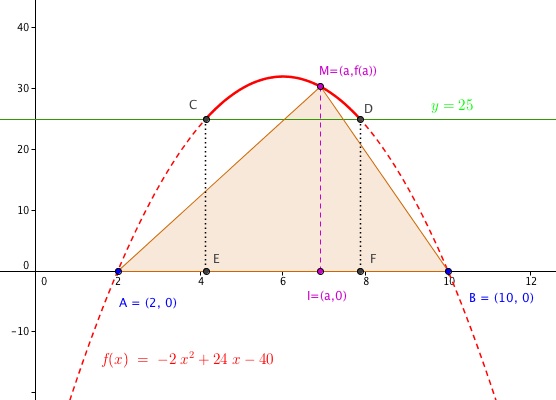
Exercice de 1ere S - Fonction pôlynome.

Posté par
Likedreamre : Exercice de 1ere S - Fonction pôlynome. 26-09-15 à 19:48

Merci de ce complément, c'est ce que j'avais fais !


Pour l'image, tu as utilisé géogébra ?

Bonne soirée

Posté par
Jedoniezhre : Exercice de 1ere S - Fonction pôlynome. 26-09-15 à 19:50

Oui, géogebra.

Posté par
mak974re : Exercice de 1ere S - Fonction pôlynome. 24-10-18 à 16:07

bonjour, comment avez-vous calculé a tout d'abord ?

Posté par
Likedreamre : Exercice de 1ere S - Fonction pôlynome. 24-10-18 à 20:33

Merci mak de votre réponse
Mais maintenant que je suis en L2 d'autres problèmes se posent à moi xD
Et je ne me rappelle plus de comment j'avais résolu ce problème
Bonne soirée

Posté par
Jedoniezhre : Exercice de 1ere S - Fonction pôlynome. 25-10-18 à 12:29

Bonjour Likedream,

Te voilà en L2 ? Bravo !

En mathématiques ?

Posté par
mak974re : Exercice de 1ere S - Fonction pôlynome. 26-10-18 à 05:19

Merci quand même

Posté par
DarkPhoenixre : Exercice de 1ere S - Fonction pôlynome. 07-11-18 à 22:00

Je pense tout de même que le bouleau n'est pas achevé. Tu n'as pas donné d'intervalle concrète dans laquelle le point M varie.


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1760 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !