Inscription / Connexion Nouveau Sujet
Exercice de trigonométrie - Course d'orientation (algorithmique)
Bonjour, voilà j'ai un exercice à faire mais je n'y arrive pas...  j'espère que quelqu'un pourra m'aider.
j'espère que quelqu'un pourra m'aider.
Voici l'énoncé:
On se place dans un plan orienté muni d'un repère (A,i,j). Le nord est indiqué par la direction du vecteur j. Pour décrire un parcours formé d'une succession de segments, on les schématise par des vecteurs. Pour une des étapes schématisée par un vecteur u, on donne la mesure principale de l'angle orienté (j,u) et la norme de u.
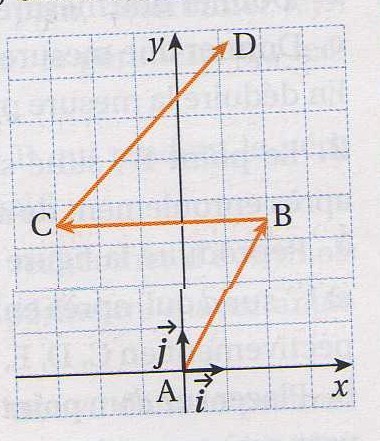
Par exemple, les indications successives (-pi/6;4), (pi/2;5) et (-pi/4;6) décrivent le parcours ABCD du schéma ci-dessous.
1. a) Calculer les coordonnées exactes du point B.
b) Décrire un algorithme qui calcule la position connaissant la précédente.
c) Calculer les coordonnées exactes des points C et D.
2. a) Décrire un algorithme qui permet d'obtenir la longueur du parcours.
b) Programmer cet algorithme à la calculatrice ou avec un logiciel.
Merci d'avance 
Bonjour, tu as la longueur AB =4 et l'angle a=( ;
; )
)
Les coordonnées de B sont les projections de AB sur ox et oy donc AB.cos( /2-
/2- /6)=4cos(
/6)=4cos( /3)
/3)
donc B(2;2 3)
3)
Pour l'algorithme, utilise
donc xn+1=xn+|Un|cos( /2+
/2+ n)
n)
et yn+1=yn+|Un|sin( /2+
/2+ n)
n)
Tu peux d'ailleurs aussi utiliser ces formules pour vérifier les coordonnées de B et calculer celles de C et D.
D'abord merci d'avoir répondu.
Les coordonnées de B sont les projections de AB sur ox et oy donc AB.cos(/2-/6)=4cos(/3)
donc B(2;23)
Dans ce que tu dis je comprend AB.cos(/2-/6)=4cos(/3) mais je ne comprend pas comment tu en déduis que B(2;23). Peux-tu m'expliquer?
Bonjour,
J'ai cet exercice à faire a la rentrée, et je n'ai pas du tout compris, meme avec la correction du 1) a
Merci de votre aide
Merci de m'avoir repondu et bonne année
Je viens de comprendre, mais je n'arrive pas a calculer les coordonnées des points C et D

 (1/2) = 2
(1/2) = 2

