Inscription / Connexion Nouveau Sujet
Exercice DM algorithme et fonction
Bonjour, j'ai un DM de maths à rendre très bientôt, et pas de chance pour moi, un exercice est un algorithme. Voici l'énoncé :
Voici un programme écrit avec le langage AlgoBox:
VARIABLES :
a EST_DU_TYPE NOMBRE
b EST_DU_TYPE NOMBRE
N EST_DU_TYPE NOMBRE
pas EST_DU_TYPE NOMBRE
d EST_DU_TYPE NOMBRE
x EST_DU_TYPE NOMBRE
k EST_DU_TYPE NOMBRE
drapeau EST_DU_TYPE NOMBRE
DEBUT_ALGORITHME :
drapeau PREND_LA_VALEUR 0
LIRE a
LIRE b
LIRE N
POUR k ALLANT_DE 1 A N
DEBUT_POUR
Si ((F1(x+pas) -(F1(x))*d<0 ALORS
DEBUT_SI
drapeau PREND_LA_VALEUR 1
FIN_SI
x PREND_LA_VALEUR x+pas
FIN_POUR
Si (drapeau==0) ALORS
DEBUT_SI
Afficher "la fonction semble monotone"
FIN_SI
SINON
DEBUT_SINON
AFFICHER "La fonction n'est pas monotone"
FIN_ALGORITHME
a) Expliquer le rôle de ce programme
b) Saisir le programme à l'orinateur et teseter son fonctionnement avec différents exmples de fonctions F1
Pour la question a) le rôle du programme est-il de démontrer qu'une fonction est monotone ou pas ? Car je suis perdu avec toutes ces variables
Merci de bien vouloir m'aider car je patauge vraiment là !

Il y a des erreurs dans l'algo
Par exemple, dans la ligne : "Si ((F1(x+pas) -(F1(x))*d<0 ALORS"
"x" n'a pas été initialisé.
"pas" n'a pas été initialisé.
"d" n'a pas été initialisé.
Il faudrait commencer par corriger ces erreurs... et les autres éventuelles.
-----
Sauf distraction. 
Ah oui autant pour moi, je l'ai mal recopié..
pas PREND_LA_VALEUR (b-a)/N
d PREND_LA_VALEUR F1(b)-F1(a)
x PREND_LA_VALEUR a
Merci beaucoup d'avoir répondu 
Mais du coup le rôle c'est de prouver que la fonction est monotone ou non? Je ne comprends le "drapeau" et "pas" en fait..
Et quand je mets des fonctios sur AlgoBox, tantôt il me met que c'est monotone, tantôt non alors que j'utilise ue même fonction, je change juste a et b mais je trouve ça incohérent ? Quelqu'un peut m'expliquer pourquoi ça fait ça ?
Bonjour,
un exemple :
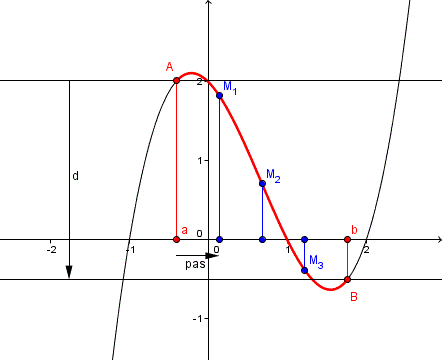
testons si la fonction "semble monotone" entre A et B
on teste si pour chaque paire de points M,M' d'abscisses x et x', on a bien f(x') - f(x) du même signe que f(b) - f(a)
et ce successivement pour
x = a et x' = a + pas
x = a + pas et x' = a + 2*pas
x = a + 2*pas et x' = a + 3*pas,
x = a + 3*pas et x' = a + 4*pas = b
ici avec N = 4 et donc pas = (b-a)/4 l'algorithme répondrait "la fonction semble monotone"
alors qu'elle ne l'est pas en réalité
c'est très exactement ce que fait cet algorithme
alors que pour une même fonction, en faisant varier a, b, N elle sorte des résultats différents selon les valeurs d'entrée n'est pas étonnant du tout
à toi de voir s'il répond correctement (toi seul connait les valeurs que tu as utilisées et la fonction f(x) que tu as utilisée...
si par contre onperend uen fon
L'algo proposé est, pour moi, foireux dans certains cas ... qui pourraient être évités.
En voila un un peu moins bancal.
VARIABLES :
a EST_DU_TYPE NOMBRE
b EST_DU_TYPE NOMBRE
N EST_DU_TYPE NOMBRE
pas EST_DU_TYPE NOMBRE
x EST_DU_TYPE NOMBRE
k EST_DU_TYPE NOMBRE
drapeau EST_DU_TYPE NOMBRE
drapeau1 EST_DU_TYPE NOMBRE
DEBUT_ALGORITHME :
drapeau PREND_LA_VALEUR 0
drapeau1 PREND_LA_VALEUR 0
LIRE a
LIRE b
LIRE N
pas PREND_LA_VALEUR (b-a)/N
x PREND_LA_VALEUR a
POUR k ALLANT_DE 1 A N
DEBUT_POUR
Si (F1(x+pas) - F1(x) < 0) ALORS
DEBUT_SI
drapeau PREND_LA_VALEUR 1
FIN_SI
SINON
DEBUT_SINON
drapeau1 PREND_LA_VALEUR 1
FIN_SINON
x PREND_LA_VALEUR x+pas
FIN_POUR
Si (drapeau == drapeau1) ALORS
DEBUT_SI
Afficher "la fonction n'est pas monotone"
FIN_SI
SINON
DEBUT_SINON
AFFICHER "La fonction semble monotone"
FIN_SINON
FIN_ALGORITHME
-----------------------
Evidemment, il est toujours possible de le prendre en défaut si N est trop petit.
Le programme initialement proposé a des défauts. (outre les lignes manquantes (il manque encore un FIN_SINON vers la fin)
En voici un évident :
Si f(a) = f(b) , alors d = 0 et donc le test "Si ((F1(x+pas) -(F1(x))*d<0 ALORS ..."
oblige le drapeau à rester à 0 et la réponse finale sera toujours "La fonction semble monotone" et ceci même si N est grand et que la fonction n'est pas monotone sur l'intervalle entré.
Tester par exemple, le cas simple F1(x) = x² et entrer a = -2 et b = 2, quel que soit N ... la réponse sera "La fonction semble monotone"
-----
Sauf distraction. 
(d'accord il manque le FIN_SINON)
mais ... le signe de f(b) - f(a) n'intervient pas ??? (distraction ?  )
)
si f(b) = f(a) la fonction est soit constante soit non monotone (on suppose qu'elle est continue)
alors il suffit de tester de façon un peu plus complexe le "si" de l'algorithme d'origine pour dire
"si le signe de f(x+pas) - f(x) est différent du signe de d"
correctement y compris quand le signe est "nul"
mais la question ici n'était pas d'améliorer l'algorithme mais pourquoi le résultat dépend des valeurs données à a et b pour une même fonction
il ne fallait pas aller plus loin que ça
l'algorithme d'origine corrigé de ses lignes manquantes oubliées suffisait sans avoir besoin de chercher à l'améliorer...
de toute façon quoi qu'on fasse on ne pourra être sûr que pour la réponse "non monotone"
le contraire étant "peut être monotone" sans qu'il soit possible d'en être sûr, quoi qu'on fasse.
Et Algobox est suffisamment "verbeux et m...ique" pour que compliquer un algorithme le rende totalement illisible
avec tous ses "ALORS", "DEBUT_trucmuche", "FIN_trucmuche" etc
surtout sans aucune indentation.
la balle est réellement dans le camp de lightning1210 sans qu'il soit besoin d'ajouter ni de modifier quoi que ce soit :
que pour une même fonction, en faisant varier a, b, N elle sorte des résultats différents selon les valeurs d'entrée n'est pas étonnant du tout
à toi de voir s'il répond correctement (toi seul connait les valeurs que tu as utilisées et la fonction f(x) que tu as utilisée...
mon post précédent n'était pas un truc pour mettre en défaut l'algorithme mais pour illustrer ce que voulait dire "pas" et pourquoi ça dépend des valeurs de a et b
pour préciser (oubli) ce que veut dire "drapeau" :
un "drapeau" est un indicateur pour mémoriser le fait que l'on a eu au moins une fois au cours de la boucle une réponse "oui" à la question :
"le signe de f(x+pas) - f(x) est-il différent de celui de d"
chaque fois qu'on répond "non" on laisse le drapeau inchangé
à la fin il vaudra 1 si on est passé au moins une fois dans la patte "oui" du SI
et 0 si on n'y est jamais passé.
(nota : ma dernière ligne était une "scorie d'édition", ligne non effacée qui trainait en dehors de la zone visible)
mathafou,
Tu as répondu à la question du 16-12-14 à 23:30
Moi, j'ai pointé les erreurs et manquements de l'algo donné dans la question initiale.
Et j'ai proposé des modifications permettant de gommer ces erreurs et manquements.
On peut, bien entendu, proposer diverses autres modifications pour corriger ces manquements.
Et si la remarque mais ... le signe de f(b) - f(a) n'intervient pas ??? (distraction ?  ) m'est adressée ...
) m'est adressée ...
Et bien non, c'est sans importance dans le programme que j'ai écrit... Si tu ne le comprends pas, tu peux toujours faire le test et constater.

oui, en relisant mieux ton algorithme (= en le relisant vraiment et pas en le survolant) on finit par comprendre ce qu'il fait .. 
On peut même facilement ajouter un petit test pour trouver, si dans le cas de la fonction qui semble monotone, la fonction semble être croissante ou décroissante.
Par exemple ainsi :
VARIABLES :
a EST_DU_TYPE NOMBRE
b EST_DU_TYPE NOMBRE
N EST_DU_TYPE NOMBRE
pas EST_DU_TYPE NOMBRE
x EST_DU_TYPE NOMBRE
k EST_DU_TYPE NOMBRE
drapeau EST_DU_TYPE NOMBRE
drapeau1 EST_DU_TYPE NOMBRE
DEBUT_ALGORITHME :
drapeau PREND_LA_VALEUR 0
drapeau1 PREND_LA_VALEUR 0
LIRE a
AFFICHER "Introduire b strictement plus grand que a"
LIRE b
TANT_QUE (b <= a) FAIRE
DEBUT_TANT_QUE
Lire b
FIN_TANT_QUE
LIRE N
pas PREND_LA_VALEUR (b-a)/N
x PREND_LA_VALEUR a
POUR k ALLANT_DE 1 A N
DEBUT_POUR
Si (F1(x+pas) - F1(x) < 0) ALORS
DEBUT_SI
drapeau PREND_LA_VALEUR 1
FIN_SI
SINON
DEBUT_SINON
drapeau1 PREND_LA_VALEUR 1
FIN_SINON
x PREND_LA_VALEUR x+pas
FIN_POUR
Si (drapeau == drapeau1) ALORS
DEBUT_SI
Afficher "la fonction n'est pas monotone"
FIN_SI
SINON
DEBUT_SINON
Si (drapeau == 1) ALORS
DEBUT_SI
Afficher "la fonction semble décroissante"
FIN_SI
SINON
DEBUT_SINON
Afficher "la fonction semble croissante"
FIN_SINON
FIN_SINON
FIN_ALGORITHME
-----
Mais ce n'est pas demandé.

non, il ne semble pas demandé d'améliorer l'algorithme en quoi que ce soit 
juste de répondre semble-t-il aux seules questions
- que fait cet algorithme, tel quel.
- le saisir, tel quel, et le tester.
et c'est déja bien assez pour cet exo de débutant en algorithmique.
qu'il manque 4 lignes (3 corrigées et le "FIN_SINON") dans la première copie initiale est très certainement une simple erreur de recopie (manuelle) de l'algorithme ici.
l'indice qu'il s'agit d'une copie manuelle est dans la casse (minuscules) de certains mots clés de Algobox : SI et AFFICHER par exemple.
un copier-coller depuis la fenêtre d'édition, ou un export en texte ne donne pas ça.


