Inscription / Connexion Nouveau Sujet
Exercice fonction
Bonjour, je n'arrive pas cet exercice :
f est la fonction définie sur R par f(x)=2x-3 et g est la fonction définie sur R - {0} par g(x)=1/x
1)Utiliser l'outil de votre choix (calculatrice,Geogebra...) pour donner le nombre de points d'intersection des courbes représentatives des fonctions f et g.
2) Déterminer les abscisses exactes de ces points.
(Indice: se ramener à une équation du second degré...)
Je ne comprend pas ce que signifie R - {0} ni l'exercice entier
Merci pour votre future aide
Bonjour
Première question
Trace les courbes
Question 2:
Belle équation à résoudre
À ta question pourquoi R-{0}
g(x)=1/x
On ne peut avoir x=0
1/0= ?
J'obtiens ça sur ma calculatrice mais je ne comprend pas pourquoi il y a 2 courbes de la fonction g et pas une et une droite pour f(x) ?
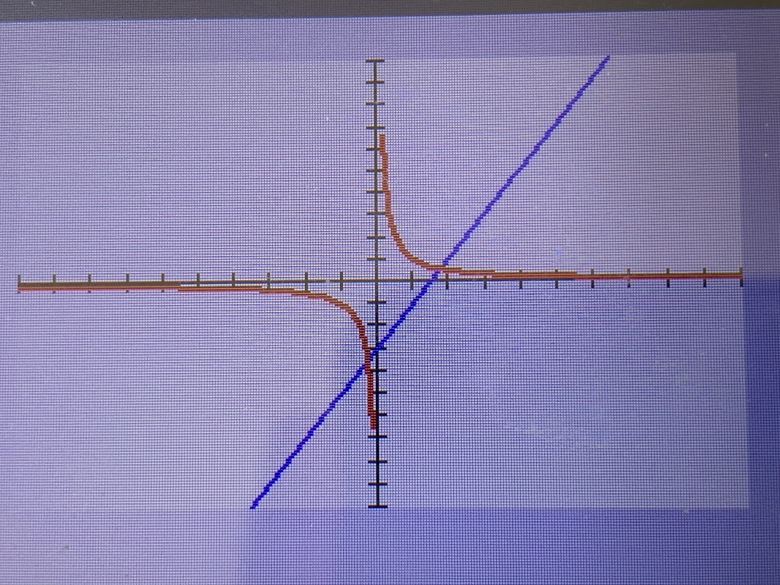
Ton image ne s'est point affichée. Fais un aperçu avant de poster.
Pourquoi 2 courbes.
1/x est une fonction inverse.
De passage
il n'y a qu'une courbe en deux morceaux il ne faut pas oublier que la fonction n'est pas définie en 0
Sur l'écran d'une calculatrice la droite est tracée
par pixels plus vous grossissez le schéma plus ils seront apparents et ne donnera plus l'impression d'une droite
Bonjour kenavo27 et je vous laisse poursuivre
Pourquoi x/1 est une fonction inverse ? Et donc lorsque la fonction est inverse il y a toujours 2 courbes ? Et le nombre de points d'intersection est donc 2 ?
kenavo27 D'accord
deux nombres sont inverses l'un de l'autre si leur produit est égal à 1
est bien l'inverse de 2 car
C'est bien pour cela que est appelée la fonction inverse
Il est bien entendu qu'ainsi 0 n'a pas d'inverse on ne peut à la fois avoir 0 et 1
Si la courbe coupait l'axe des ordonnées on aurait alors une image pour 0 ce qui est impossible donc la courbe est bien en deux morceaux
il en est de même à chaque fois que la fonction n'est pas définie pour une valeur
D'accord donc pour la question 1) je dois juste dire que le nombre de points d'intersection est 2(si c'est bien le cas) entre g(x) et f(x) ? Je ne dois pas refaire le graphique, dire qu'il s'agit d'une fonction inverse, que la courbe de la fonction est une hyperbole ou autre ?
Dire seulement que d'après le graphique, les courbes se coupent en deux points
le reste est du superflu valable seulement pour vous, pour être sûr que vous ne vous êtes pas trompé
Si l'on sait que la courbe est une hyperbole on sait l'allure qu'elle a si cela ressemble plus à une parabole c'est qu'on s'est trompé quelque part
Oui vous dites que vous formez l'équation aux abscisses des points d'intersection
et comme vous pouvez multiplier les deux membres par
Comment dois-je faire pour calculer f(x)=g(x) ?
Je commence par arranger l'équation pour obtenir quelque chose =0 ? Donc en déplaçant 1/x à gauche ? (mais comment ?)
Oui
il n'y a pas de changement dans la résolution des équations
on ajoute aux deux membres ou on le fait implicitement
On obtient donc ce trinôme du second degré ?:
2x^2-3x-1=0
c'est bon ?
Et donc ensuite s'il vous plaît ?
Delta=17 l'équation admet donc 2 racines réelles distinctes
X1=(formule)=1,8(environ)
x2=(formule)=-0,3(environ)
Les points d'intersection sont donc aux abscisses 1,8 et -0,3
Est-ce que je devrai mettre 1,78 et -0,28 comme arrondi ou laisser 1,8 et -0,3 ?
Ni l'un ni l'autre
Le texte :« Déterminer les abscisses exactes de ces points. »
Il faut donc garder la racine carrée
Ce seront les abscisses des points d'intersection des deux courbes
Ce n'est pas parce que vous avez ajouté quelques décimales que cela en fait une valeur exacte .
La valeur exacte de est
.
Vous pouvez mettre 500 décimales que cela ne sera qu'une valeur approchée
Ah d'accord merci mais je peux l'écrire 2 fois, un avec un + et l'autre avec un - he ne suis pas obligé de faire comme vous en mettant le + et - ensemble ? D'ailleurs que signifie ce sign me ?
Bien sûr c'est juste un raccourci pour les deux plus ou moins telle ou telle valeur
mais vous mettez les deux valeurs


