Inscription / Connexion Nouveau Sujet
Exercice fonction racine carée, variables et géogébra
Bonjour!
J'ai cet exercice à réaliser pour demain et je bloque!
Voici l'énoncé:
Un plan est rapporté au repère orthonormé (0; i; j). Soit un point A (a;0) où a est un réel positif.
On construit successivement:
-Les points B(a-1;0) et C(2a;0)
- Le cercle C de diamètre [BC]
-La droite (d) perpendiculaire à (BC) passant par A
--Le point M, d'ordonnée positive, situé à l'intersection du cercle C et de la droite (d)
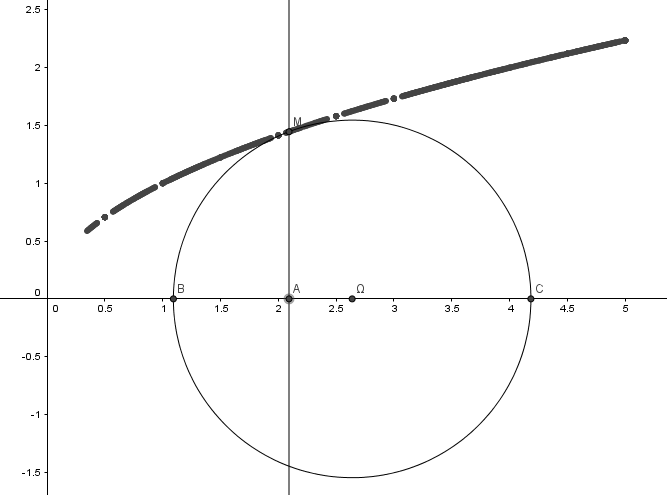
1. Réaliser une figure à l'aide de Géogébra (question déjà faite)
2. Quelle semble être la nature de la courbe décrite par le point M lorsque le point A se déplace le long de l'axe des abscisses? (J'ai répondu qu'elle semblait être la représentation de la fonction racine carrée)
Voici les questions sur lesquelles je bloque:
3. Exprimer la distance AM en fonction de a (on pourra penser a utiliser le théorème de pythagore dans les trois triangles, ou bien la trigonométrie)
4. En déduire que le lieu des points M quand A se déplace le long de l'axe des abscisses est la représentation graphique d'une fonction de référence que l'on déterminera.
Merci d'avance!
hekla, comment as-tu fait pour construire un cercle sur géogébra avec seulement le diamètre? (j'ai fait l'erreur d'utiliser le rayon au lieu du diamètre malheureusement)
Je pensais prendre le triangle BAM comme base pour pythagore, mais qu'en faire?
il n'a pas été dit : le cercle de centre A mais le cercle de diamètre [BC]
1 construction du milieu de [BC]
2 cercle dont on connaît le centre et un point
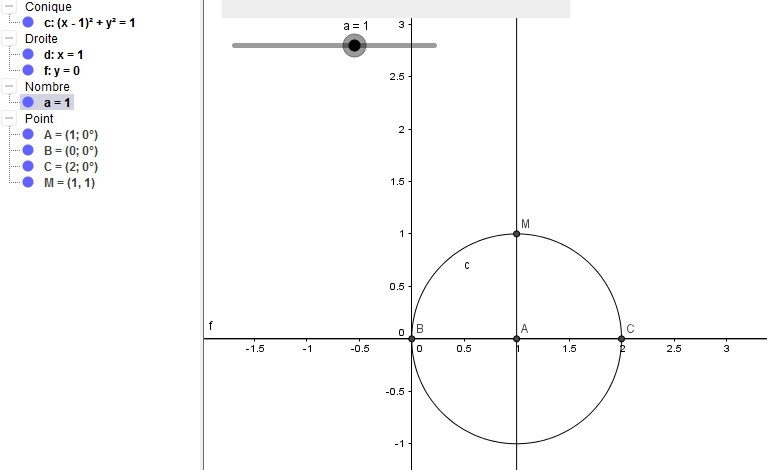
il faut faire bouger le curseur car pour a=1 B est en O ce qui peut être gênant
En utilisant pythagore dans les triangles BMC, BAM et MAC, que puis-je faire? Je ne comprends pas l'intérêt d'utiliser 3 triangles....
Bonjour,
je réalise que mon dessin est faux...
on ne peut pas en juger car ta valeur particulière de a (=1) ne permet de rien dire du tout.
si ça se trouve il est parfaitement juste
simplement le proposer dans ce cas particulier masque bien trop de choses.
par contre il est effectivement faux dans ce sens que sur Geogebra les coordonnées doivent être séparées par des VIRGULES et pas des points virgules comme en maths "Françaises"
cet absurde point virgule français étant la conséquence en français et uniquement en français de l'existence d'une "virgule décimale" légalement obligatoire qui modifie toute la ponctuation normale (normale dans le reste du monde et dans les logiciels)
le point virgule dans les coordonnées de Geogébra veut dire "en coordonnées polaires" !!
et de même une virgule décimale doit être écrite avec un point décimal sur Geogebra etc
(etc veut dire en Algobox, en Scratch, en JavaScript, en XCas etc etc)
mathafou, cela à t'il un impact dans mon exercice?
kenavo 27, oui, c'est une "conique" (notion jamais vue), variable en fonction de a.
oui et non.
les coordonnées de A ne sont pas rayon = a et angle = 0 degré mais x = a et y = 0 ce qui doit s'écrire (a, 0)
ça ne changera pas vraiment grand chose ici (parce que 0 degrés c'est pareil que y = 0, c'est sur l'axe des abscisses, par coup de bol) mais c'est une habitude à prendre systématiquement, de noter les coordonnées dans géogébra avec des virgules.
kenavo ne te demandait pas "as tu vu dans la fenêtre algèbre de Géogebra"
mais as tu vu en cours l'équation d'un cercle...  (pas d'une conique en général, c'est hors programme)
(pas d'une conique en général, c'est hors programme)
à défaut de connaitre l'équation d'un cercle (en général) tu vas calculer les coordonnées de M simplement par le bon vieux Pythagore ...
(c'est en fait par ce bon vieux Pythagore qu'on obtient en général l'équation du cercle !!)
Je devine que son ordonnée est la racine de son abscisse, mais comment l'expliquer? avec ça je peux utiliser MB[/sup]=MA[sup]=AB[sup][/sup]
?
Je n'ai pas compris... quel pythagore utiliser? dois je faire AM=sous racine (Xm-Xa)carré+(Ym-Ya)carré (formule vue en seconde?)
Voici ce que j'essaye: MC²=MA²+AC²
on a M(a; racine de a) car MA perpendiculaire a BB
C (2a;0)
A(a;0)
Je cherche la distance MC:
MC=(sous racine)(xc-xm)²+(yc-ym)²
=(sous racine)(2a-a)²+(0-racine de a)
=(sous racine)a²+(-racine de a)
oh, je realise que je ne peux pas calculer une double racine!
mais comment trouver les coordonnées de oméga?
Oui, j'y suis! mais comment trouver les coordonnées de oméga? j'ai compris la méthode, c'est tout ce qui me manque
Bonjour,
A une certaine époque, on apprenait au collège que:
La hauteur d' un triangle rectangle issue de l' angle droit est moyenne proportionnelle entre les segments qu' elle détermine sur l' hypoténuse.
Autrement dit,

Bonjour lake
il me semble que cela se voyait en quatrième avec les triangles semblables
cela fait quelques lustres que la géométrie a presque disparu.
de nos jours la géométrie est réduite au strict minimum
les diverses relations métriques "exotiques" dans un triangle rectangle sont donc passées à la trappe depuis longtemps et il reste exclusivement Pythagore et rien d'autre
si on en a besoin quelque part, on les redémontre au coup par coup.
de toute façon écrire que xΩ = (xB + xC)/2 puis que ΩA2 = (xA-xΩ)2 + (0-0)2 est plus dans l'esprit de nos jours ...
(ou ΩA avec la racine carrée, mais comme on s'en sert pour l'élever au carré ensuite ...)
Je ne comprends malheureuement toujours pas, même en regardant la figure! Pourriez vous m'expliquer?
B(a-1);0) À(à;0). C(2a;0)
 est milieu de BC
est milieu de BC
Donc l'abscisse de  = (a-1+2a)/2= (3a-1)/2
= (a-1+2a)/2= (3a-1)/2
Distance du rayon : xC-x =........
=........
Distance A =x
=x -xA=.....
-xA=.....
Tu as tout maintenant
la méthode "brute" avec les coordonnées est plus directe ici et évite de se poser quelques questions "philosophiques"
(que de voir que avec des points alignés, les mesures des segments s'ajoutent ou se retranchent, du moment qu'on connait dans quel ordre sont les points)
attention que quand on parle de distance ce sont des nombres forcément positifs
donc à moins de justifier de l'ordre des points quel que soit la valeur de a, il faut écrire des valeurs absolues :
Distance du rayon : |xC-x
 | =........
| =........
Distance A
 = |x
= |x -xA| =.....
-xA| =.....ces valeurs absolues disparaitront quand on écrira ces trucs là au carré dans Pythagore
mais c'est à ça que je faisais référence en parlant de "questions philosophiques"
Bien, je commence à comprendre... Lorsque j'ai omégaM et omégaA, j'ai AM en utilisant pythagore. C'est super! Je vous remercie tous!
Oui, merci! Mais je ne comprends pas comment se fait t'il que la mesure de la distance se résume à cela? Le calcul n'est t'il pas d'habitude beaucoup plus long pour la distance entre deux points sur un repère?