Inscription / Connexion Nouveau Sujet
exercice gémétrie
Bonsoir, je viens pour demander de l'aide sur un exercice que je ne comprend pas du tout et où j'ai cruellement besoin d'aide .
Voici l'énoncé:
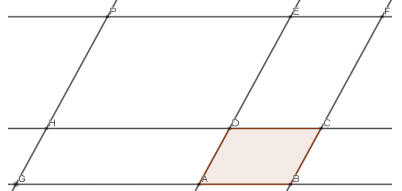
ABCD est un parallélogramme, et P un point du plan distinct de B et de D.
La parallèle à (AB) passant par P coupe (AD) en E et (BC) en F.
La parallèle à (AD) passant par P coupe (AB) en G et (CD) en H.
On veut montrer que les droites (EH), (F G) et (AC) sont concourantes ou parallèles.
On se place dans le repère (A; vecteurAB;vecteur AD)
1. Donner les coordonnées des points A, B, C et D.
2. On suppose que P(−2; 3). (voir figure)
(a) Déterminer les coordonnées des points E, F, G et H.
(b) Montrer que (EH), (F G) et (AC) sont parallèles.
3. On suppose dans cette question que P a pour coordonnées (5; -2).
a) Déterminer une équation cartésienne de la droite (AC).
b) Démontrer que 3 x - 5 y - 10=0 est une équation cartésienne de (EH).
c) Déterminer les coordonnées du point I, intersection des droites (AC) et (EH).
d) Démontrer que I appartient à (FG).
e) Que peut-on dire des droites (EH) , (FG) et (AC) ?
On pose à présent P (a ; b) avec a et b deux réels.
4. Exprimer les coordonnées des points E, F, G et H en fonction de a et b.
5. Démontrer que (1 - b) x - a y+a b=0 est une équation cartésienne de (EH).
6. On suppose que a+b≠1 .
a) Démontrer que les droites (AC) et (EH) sont sécantes en un point que l'on nommera M.On donne M (ab/a+b- 1 ; ab/a+b−1)
b) Justifier que (FG) est sécante avec (AC) et (EH) puis montrer que M appartient à (FG)
voici mes réponses:
1) A(0;0) B(1;0) C(1;1) D(0;1)
2)a)E(0;3) F(1;3) G(-2;0) et H(-2;1)
b)Pur démontrer que (EH) (FG) et (AC) sont parallèles on peut se servir des vecteur EH FG et AC. Et si ces vecteurs sont colinéaires, les droites seront donc parallèles :
vecteurEH (-2-0 (-2
1-3) -2)
vecteurFG (-2-1 (-3
0-3) -3)
vecteurAC(1-0 (1
1-0) 1)
det(vecteurEH,vecteurFG)=(-2) x (-3) - (-2) x (-3) = 0
det(vecteurEH,vecteurAC)=(-2) x 1 - (-2) x 1 = 0
Donc (EH) (FG) et (AC) sont parallèles
3)a)Pour déterminer une équation cartésienne de la droite (AC), j'ai décidé d'utiliser le vecteur directeur AC (1
1)
ce qui me donne x-y+c=0
puis j'essaye de trouver c en utilisant les coordonnées du point C:
c=0
donc l'équation cartésienne est de y=x
b) si P(5;-2), alors E(0; -2) et H (5;1)
pour vérifier si 3 x - 5 y - 10=0, on remplace x et y par les coordonnées des points E et H:
point E: 3 x 0 - 5 x (-2) - 10= 0
point H: 3 x 5 - 5 x 1 - 10= 0
Donc 3 x - 5 y - 10=0 est bien une équation cartésienne de (EH)
c)pour déterminer les coordonnées du point I, j'utilise un système:
y=x
3x - 5y -10 =0
y=x
x=-5
donc I(-5;-5)
Et c'est pour l'instant tout ce que j'ai réussi à faire, le reste je ne sais vraiment pas comment procéder... Car pour la plupart de que je viens de faire je ne vais pas mentir je me suis aidée d'internet, mais je n'ai toujours pas l'impression d'avoir compris ce que j'ai fais.Merci d'avance pour votre aide.
Bonjour,
2a) tu ne précises pas comment tu as déterminé les coordonnées de ces points.
3a)
Pour déterminer une équation cartésienne de la droite (AC), j'ai décidé d'utiliser le vecteur directeur AC
Ok
ce qui me donne x-y+c=0 ????
soit M(x,y) un point appartenant à la droite AC
les vecteurs AM et AC
sont coliénaires
ce qui te permet de déterminer une équation de la droite (AC)
calcul à effectuer
b) si P(5;-2), alors E(0; -2) et H (5;1) coordonnées à justifier
puis déteminer une équation de la droite (EH) ( pas vérifier que..)
Bonjour! Déjà merci de votre réponse je vais essayer d'appliquer ce que vous m'avez dit.
2)a)
Point E : La parallèle à (AB) passant par P coupe (AD) en E , on sait donc que yE=yP=3.
Puis on sait que E E (AD) donc xE=xE=0
E(0;3)
Point F: La parallèle à (AB) passant par P coupe (BC) en F, on sait donc que yF=yP=3
Puis on sait que F E (BC) donc xF=xB=1
F(1;3)
Point G : La parallèle à (AD) passant par P coupe (AB) en G, on sait donc que xG=xP=-2
Puis on sait que G E (AB) donc yG=yA=0
G(-2;0)
Point H: La parallèle à (AD) passant par P coupe (CD) en H, on sait que xH=xP=-2
Puis on sait que H E (CD) donc yH=yD=1
H(-2;1)
3)a) Pour cette question je ne suis pas sûre d'avoir compris. Il faut utiliser M, mais je ne comprend pas bien comment et pourquoi. En fait peut être que j'ai mal expliquer ce que j'ai fait. Dans ma réponse précédent j'avais tout simplement remplacer les coordonnées du vecteur AC dans ax+by+c=0, car je sais qu'un vecteur directeur u(-b, et que vecteurAC est directeur de (AC).
a)
Ce qui m'a amené à x-y+c=0
Je ne sais pas si on comprend ce que j'avance et si ça marche..
3)b)Point E: on sait que P(5;-2), comme P E à (EF), yE=yP=-2, et que E E (AD) donc xE=xA=0
E(0;-2)
Point H: xH=xP=5 car P E (GH). H E à (DC) donc yH=yD=1
H(5;1)
Pour démontrer que 3 x -5y -10 =0 est une équation de la droite (EH) , on remplace les coordonnées de E puis de H dans l'équation :
3 x 0 - 5 x (-2) -10 = 0
E vérifie cette équation
3 x 5 - 5 x 1 - 10 = 0
H vérifie cette équation
3 x -5y -10 =0 est bien une équation de la droite (EH)
voilà j'ai essayé de corriger mes erreurs j'espère que c'est un peu mieux comme ça
OK pour 2a)
3a) Tu dois avoir dans ton cours : ( collège.)
Si les vecteurs (AM) et ( AC) sont colinéaires , alors M appartient à la droite (AC)
Le vecteur et le vecteur
sont colinéaires si et seulement si XY'-YX'=0
ah oui si ça remonte au collège je ne pense pas trop m'en rappeler :')) mais je pense avoir compris
3)a) Soit M(x;y), un point appartenant à la droite AC, les vecteurs AM(x
y)
et AC(1 sont colinéaires seulement si xy'-yx'=0, donc:
1)
x * 1- y * 1 =0
y=x
Est ce que expliquer comme ça ma phrase est juste? Et si j'ai bien compris pour trouver l'équation d'une droite, il faut toujours placé un point M(x;y) et appliquer le formule du déterminant?
D'accord merci énormément! 
et du coup e vais essayer de continuer les questions, vu que maintenant tout me paraît plus clair.
3)c) pour déterminer les coordonnées du point I, j'utilise un système:
y=x
3x - 5y -10 =0
y=x
x=-5
donc I(-5;-5)
d) Point F : on sait que P(5;-2) et comme P E (EF), yF=yP=-2
on sait que F E (BC), donc xF=xB=1
F(1;-2)
Point G: o,n sait que P(5;-2) et comme P E (GH), xG=xp=5
on sait que G E (AB) donc yG=yA=0
G(5;0)
Pour démontrer que I appartient à (FG), il suffit de démontrer que vecteurFI et vecteur FG sont colinéaires:
vecteurFI (-5-1 (-6
-5+2) -3)
vecteurFG (5-1 (4
0+2) 2)
det(vecteurFI;vecteurFG)= -6 x 2 - (-3) x 4 =0
Donc I E (FG) car vecteurFI et vecteurFG sont colinéaires, donc F I et G sont alignés.
e)On peut dire que (EH),(FG) et (AC) sont concourantes en I, car elles passent toutes par le point I.
J'espère que tout est bon pour ce que je viens de faire! Je vais essayer de faire les autres questions je les mettrai ici plus tard! encore un grand merci PLSVU 
Merci beaucoup j'espère que tout se passera bien!
Voici du coup ce que j'ai fait pour les dernières questions. Pas besoin forcément de regarder les questions 4 et 5, car je les ai plutôt bien comprises, j'ai plus de problèmes avec la 6.
4)P(a;b)
Point E : La parallèle à (AB) passant par P coupe (AD) en E , on sait donc que yE=yP=b.
Puis on sait que E E (AD) donc xE=xE=0
E(0;b)
Point F: La parallèle à (AB) passant par P coupe (BC) en F, on sait donc que yF=yP=b
Puis on sait que F E (BC) donc xF=xB=1
F(1;b)
Point G : La parallèle à (AD) passant par P coupe (AB) en G, on sait donc que xG=xP=a
Puis on sait que G E (AB) donc yG=yA=0
G(a;0)
Point H: La parallèle à (AD) passant par P coupe (CD) en H, on sait que xH=xP=a
Puis on sait que H E (CD) donc yH=yD=1
H(a;1)
5) Pour démontrer que (1 - b) x - a y+a b=0 est une équation de la droite (EH) , on remplace les coordonnées de E puis de H dans l'équation :
(1 - b) x 0 - a x b +a b=0
E vérifie cette équation
(1 - b) x a - a x b +a b=0
H vérifie cette équation
(1 - b) x - a y+a b=0 est bien une équation de la droite (EH)
6) a) On sait que AC a pour équation y=x, et que EH a pour équation (1 - b) x - a y+a b=0, on peut donc mettre en place un système:
y=x
(1 - b) x - a * x +a b=0
y=x
(1-b-a)x=-ab
y=x
x=-ab/1-b-a
et c'est à ce moment là que je bloque, j'arrive pas du tout à trouver mon erreur. Je suis sensée trouver ab/a+b-1, mais je trouve le contraire j'ai l'impression . Je suis vraiment désolé de vous déranger encore
Pour démontrer que (1 - b) x - a y+a b=0 est une équation de la droite (EH) , on remplace les coordonnées de E puis de H dans l'équation :
pour moi ,c'est plutôt on vérifie que ....
.
avec des parenthèses
x=-ab/(1-b-a) =..........
je pense que tu sais que
-3/(-5)=3/5
tu ne me déranges pas .
ah bah zut c'était tout simple en fait :'))
Et du coup j'ai essayé de réfléchir par rapport à la 6b et du coup pour prouver que par exemple (FG) et (AC) sont sécantes, on doit prouver qu'ils sont colinéaires ?
6. On suppose que a+b≠1 .
a) Démontrer que les droites (AC) et (EH) sont sécantes en un point que l'on nommera M.On donne M (ab/(a+b- 1) ; ab/(a+b−1)
b) Justifier que (FG) est sécante avec (AC) et (EH) puis montrer que M appartient à (FG)
Quand tu résous le système
{y=x
{(1 - b) x - a x +a b=0
tu ne précises pas pourquoi le point M est toujours défini ?
Désolé de mon retard, j'étais en cours ! Et je n'ai pas bien compris, comment ça préciser que le point M est toujours défini quand je résout ce système ?
Ah oui c'est bon je crois avoir compris! comme on a donné a+b différent de 1, le point M est défini car si on fait a+b-1, on sait que ça ne sera pas égal à 0 vu que la valeur 1 est interdite en quelque sorte donc b sera toujours différent de 0 dans ce cas là. Est ce que c'est bien ça?
Merci encore de m'avoir aidée grâce à vous j'ai compris mon dm!  ))
))
En tout cas je pense avoir mieux réussi les questions que si j'avais suivi mon raisonnement parfois pas très logique… Encore un grand merci!
Prenez soin de vous, j'espère que le reconfinement ne sera pas trop dur!
Oui je l'ai terminé, je vais vous mettre ce que j'ai fais!
6)b) On sait que vecteurAC(1;1), puis on calcule vecteurFG:
vecteurFG(a-1)
(-b)
ensuite pour prouver que FG et AC sont sécantes on utilise la formule du déterminant avec les vecteurs
1 x (a-1)-1 x (-b)=0
a+b=0
Donc FG et AC sont bien sécantes; et j'ai la même chose avec EH
Pour montrer que M E à FG, on utilise les vecteur FG et GM:
GM(-a^2-a/a+B-1)
ab/a+b-1
Puis on cherche le det des vecteurs:
detFG;GM = (-a^2-a/a+B-1) x (-b) - ab/a+b-1 x (a-1)
=0
Donc M appartient à FG
Désolé si j'ai mis si peu de précision mais ça sonne bientôt et je vais devoir rendre mon dm :'))) ?Je vous tiendrai au courant de ma note! 
erreurs de frappe ...pour le signe =
ensuite pour prouver que FG et AC sont sécantes on utilise la formule du déterminant avec les vecteurs
1 x (a-1)-1 x (-b)= a-1+b =a+b-1≠0 puisque a+b≠1
a+b=0
les vecteurs ne sont pas colinéaires les droites (FG) et (AC) sont sécantes
Idem (EH)et (FG)
a(-b)-(1-b)(a-b)===>-a-b+1≠0 puisque a+b≠1
les vecteur FM et FG sont colinéaires
OK pour det =0===> M appartient à (FG)
ah je vois, en fait j'ai fais une faute de frappe! C'est bien a+b=1 que j'ai trouvé, sauf que je n'ai pas mis la justification avec a+b différent de 1. Bon bah j'ai déjà rendue ma copie mais l'essentiel c'est que j'aurai au moins compris pour la prochaine fois  Vos explications m'ont vraiment aidés à mieux comprendre!
Vos explications m'ont vraiment aidés à mieux comprendre!


