Inscription / Connexion Nouveau Sujet
Exercice maths
Bonjour,
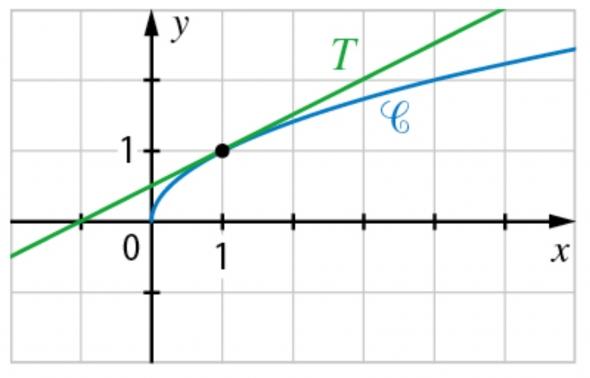
La courbe C de la fonction f définie sur [0;+infini[ par f(x)=racine carrée de x
et sa tangente T au point d'abscisse 1 (Photo)
1) a) déterminer f'(1) par lecture graphique
b) retrouver ce résultat par un calcul
2) Reproduire la courbe C puis tracer sa tangente T au point d'abscisse 1
3) La courbe C admet elle une tangente parallèle a la droite d'équation y=2x-5 ?
Si oui, déterminer les coordonnées du point de contact
4) Expliquer pourquoi aucune tangente de C n'a une pente négative
Merci
Bonjour,
1a) tu dois savoir la relation qu'il y a entre la dérivée et la pente d'une tangente ... (alias son coefficient directeur) voir cours
il te reste donc à déterminer graphiquement le coefficient directeur de la tangente tracée ...
1b) ... bein ... calculer la dérivée (cours)
Bonsoir,
J'ai fait la question 1) a) et b)
1) a) Par lecture graphique, f'(1) = 1/2
Il s'agit de la pente de la tangente: prenons les points de coordonnées (-1 ; 0) et (1 ; 1), la pente donne : ?y/?x = (1 - 0)/(1-(-1)) = 1/2
b) Par calcul, on a :
* Sylvieg > Image effacée. Merci d'utiliser les outils mis à ta disposition pour écrire les formules mathématiques  *
*
sauf que on demande de le refaire (à la main sur papier)
faire une table de valeurs, reporter les points et tracer à main levée une courbe "harmonieuse" reliant ces points
la tangente en (1; 1) déja connue, et tracée au préalable à la règle, guide pour ce tracé.
il vaut donc mieux tracer la tangente avant la courbe que après !


