Inscription / Connexion Nouveau Sujet
Exercice optimisation application de dérivation
Bonjour à tous je suis en classe de 1èreG avec la Spécialilté math, alors d'abords je vais vous montrer l'énoncer que verrez avec l'image que j'ai inséré.
Donc mon problème est que dans la 2ème question on me demande de montrer que
la fonction S(x) = pi/4(12x-x^2) je ne sais comment m'y prend et j'ai vraiment besoins d'aide la réponse ne m'intéresse pas j'aimerais que vous m'apportiez des suggestions et de l'aide Sur ceux merci au revoir et à bientôt.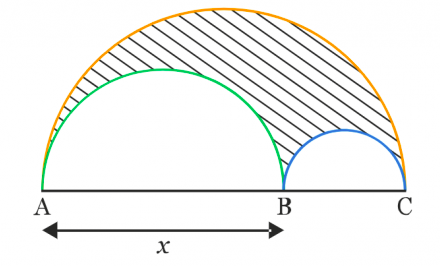
* malou > si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum. *
Sujet ancien- ne plus donner ce lien-merci
aah d'accord pardon donc voici l'énoncé:
[AC] est un segment de longueur 12 cm. B est un point du segment [AC] tel que AB=x.
On construit d'un même côté de la droite (AB) les demi-cercles de diamètres [AB], [BC] et [AC].
On note S(x) l'aire de la surface hachurée en fonction de x
calcule l'aire du demi-cercle de diamètre AC
et tu enlèves les deux autres
ça doit se faire ça ...
tu essaies
d'accord alors:
Aire total = ((pi*6^2)/2)-(pi*(x/2)^2)/2)+(pi*(x/2)^2/2))
ça doit être ça alors non ?
Bonsoir,
Aire totale= ((pi*6^2)/2)-(pi*(x/2)^2)/2)+(pi*(x/2)^2)/2) faux
l'aire " du cercle bleu " est fausse
je n'aurais pas du parler de l'aire du demi-cercle, mais aurais du parler de l'aire du demi-disque...
ah non si je pense que c'est ça attendez:
Aire total = ((pi*6^2)/2)-((pi*(x/2)^2)/2)+(pi*(12-x)^2/2)/2))
c'est un peu illisible ton truc là...
tu sais qu'un disque a pour aire pi*r² ou ici mieux pi*d²/4
et en 1 seule ligne, tu as ton résultat sans tous ces échafaudages de fractions
pourquoi le /4 tout au bout de la ligne
on est sur des demi-disque, pas des quart de disque
le reste me semble OK
tu développes tous les numérateurs, et tu vas trouver ton résultat
ben là tout seul tu devrais t'en sortir...est-ce la même chose que dans l'énoncé ? non...donc retrouver l'erreur ....
D'accord donc si je reprends votre formule ça donne ça:
[ (pi*12^2/4)-((pi*x^2)/4+(pi*((12-x)^2)) ]/4)
ce n'est pas "ma" formule !
écris le détail de tes calculs si tu ne trouves pas mais par pitié ne joue pas aux devinettes...
Bon voilà comment je m'y suis pris,
Dans premier temps, j'ai développé l'expression de l'énoncer.
Ce qui m'a donné :
S(x)=π/4(−x^2+12x)
S(x)=−1/4πx^2+3πx
Ensuite, je me suis dis que si l'expression développer de l'énoncer est égal à cette formule:
((pi*12^2)/4)-(((pi*x^2)/4+(pi*(12-x)^2)/4)/2) qui est égale à (en développant):
−1/4πx^2+3πx+18π alors j'ai réussi à montrer que l'expression est bien égale à:
S(x) = π/4(12x-x^2)
Sauf que là, il y a le +18π qui gêne alors est ce que je devrais considérer que l'expression développer de la formule est bien égal à l'énoncer ou c'est complètement faux?
Je suis sincèrement désoler si je vous fais perdre du temps ainsi et que je n'arrive pas à trouver le calcul qui semble être évident.
Bon voilà comment je m'y suis pris,
Dans premier temps, j'ai développé l'expression de l'énoncer.
Ce qui m'a donné :
S(x)=π/4(−x^2+12x)
S(x)=−1/4πx^2+3πx
Ensuite, je me suis dis que si l'expression développer de l'énoncer est égal à cette formule:
((pi*12^2)/4)-(((pi*x^2)/4+(pi*(12-x)^2)/4)/2) qui est égale à (en développant):
−1/4πx^2+3πx+18π alors j'ai réussi à montrer que l'expression est bien égale à:
S(x) = π/4(12x-x^2)
Sauf que là, il y a le +18π qui gêne alors est ce que je devrais considérer que l'expression développer de la formule est bien égal à l'énoncer ou c'est complètement faux?
Je suis sincèrement désoler si je vous fais perdre du temps ainsi et que je n'arrive pas à trouver le calcul qui semble être évident.
mets moi tes calculs, je veux voir où
pars de là
[ (pi*12^2/4)-((pi*x^2)/4+(pi*((12-x)^2)) ]/4)
et n'oublie pas : moins on en écrit, moins on a de chance de se tromper
quand on sait calculer, ça tient en très peu de lignes
en utilisant la formule pour l'aire des 1/2 disques
S=aire 1/2 disque jaune - aire du 1/2 disque vert -aire du 1/2 disque bleu
tu te trompes manifestement en développant
mets moi tes calculs, je veux voir où
pars de là
[ (pi*12^2/4)-((pi*x^2)/4+(pi*((12-x)^2)) ]/4)
et n'oublie pas : moins on en écrit, moins on a de chance de se tromper
quand on sait calculer, ça tient en très peu de lignes
en utilisant la formule
S=aire 1/2 disque jaune - aire du 1/2 disque vert -aire du 1/2 disque bleu
=
/8⋅[122−x^2−(−x+12)^2]=
=1/8⋅[(−x^2+144)−(x^2−24x+144)]=
=1/8⋅[−2x2+24x]=
=(1/4*1/2)(2*(-x^2+12x))=
=−1/4x2+3x
le résultat c'est ça alors ?
en utilisant la formule
S=aire 1/2 disque jaune - aire du 1/2 disque vert -aire du 1/2 disque bleu
=
/8⋅[122−x^2−(−x+12)^2]=
=1/8
⋅[(−x^2+144)−(x^2−24x+144)]=
=1/8
⋅[−2x2+24x]=
=(1/4
*1/2)(2*(-x^2+12x))=
=−1/4
x^2+3x
le résultat c'est ça alors ?
Merci d'avoir essayer de m'aider je pense que vais m'entraîner à réduire des expressions littéral pour m'améliorer.
en facteur pour l'écrire comme dans l'énoncé
Annuler
connectez vous