Bonjour, alors voila je suis bloqué à cet exercice, plus précisément à la question deux, je ne pense pas avoir toutes les données nécessaires pour pouvoir calculer les probabilités. Si jamais vous pourriez m'aider, merci d'avance!

Exercice 3
Pour rejoindre le sommet S d'une montagne des Alpes à partir d'un point de départ D, un randonneur
a la possibilité d'emprunter plusieurs itinéraires. Le parcours n'étant pas faisable en une journée, il doit passer une nuit dans l'un des deux refuges se trouvant à la même altitude de 1 400 mètres sur les itinéraires existants : les deux refuges ne sont pas situés au même endroit. On les appelle R1 et R2. Le lendemain matin, pour atteindre le sommet qui se trouve à 2 500 mètres d'altitude, le randonneur a deux possibilités : il peut atteindre le sommet en faisant une halte au refuge R3, ou bien atteindre directement le sommet
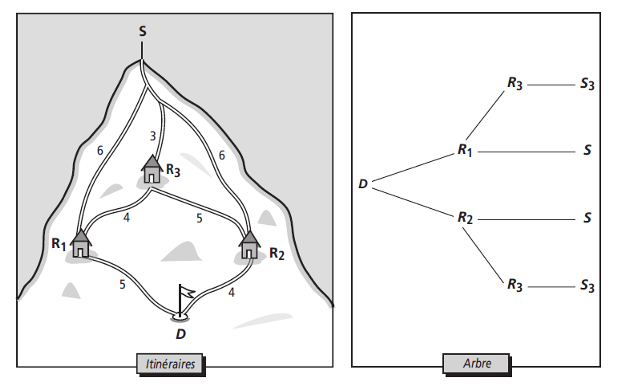
(voir schéma tout en bas de l'exercice).

On sait que :

La probabilité que le randonneur choisisse de passer par R1 est égale à 1/3;

La probabilité de monter directement au sommet depuis R1 est égale à 3/4;

La probabilité de monter directement au sommet depuis R2 est égale à 2/3.

Question 1
On désigne par R1 l'événement « le randonneur s'arrête au refuge R1 », et on note de même les événements R2 et R3.
On note S3 l'événement « le randonneur arrive au sommet après s'être arrêté au refuge R3 » et S l'événement « le randonneur arrive au sommet sans s'être arrêté au refuge R3 ».
Reproduire et compléter l'arbre pondéré montrant les trajets possibles.

Question 2
À l'aide de l'arbre pondéré déterminer :

la probabilité que le randonneur ait fait une halte au refuge R3 sachant qu'il a passé la nuit au refuge R1;

la probabilité que le randonneur ait fait une halte au refuge R3;

la probabilité que le second jour le randonneur soit monté directement au sommet.

Question 3
On note MN la distance à parcourir, exprimée en km, pour se rendre d'un point M à un point N.
On sait que : DR1-5, DR2-4, R1R3-4, R2R3-5, R1S-6, R2S-6, R1S-3.

Soit X la variable aléatoire représentant la distance parcourue par un randonneur pour aller du départ D au sommet S.

a)
A l'aide de l'arbre, déterminer la loi de probabilité de X.

b)
Calculer l'espérance mathématique de X. En donner une interprétation.