Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. PremièreForum de première [tout]Lister tous les topics de mathématiques
Niveau première
Partager :

exercice produit scalaire

Posté par
life 19-02-12 à 22:06

***

je ne sais pas comment faire l'exercice 1 la question 2 . donc si quelqu'un pouvait me donner des piste ce serais bien
* Océane > life si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum. *

Posté par
dhaltere : exercice produit scalaire 19-02-12 à 23:33

à mon avis, un produit scalaire nul devrait faire l'affaire...

Posté par
lifere 20-02-12 à 17:42

a ok océane .

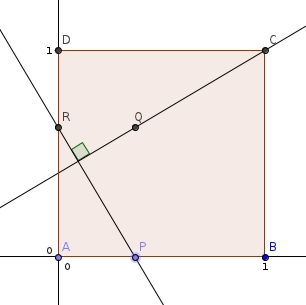
Soit un carré ABCD. On construit un rectangle APQR tel que :
·  P et R sont sur les côtés [AB] et [AD] du carré
·  AP = DR
Le problème a pour objet de montrer que les droites (CQ) et (PR) sont perpendiculaires.

1. Justifier que : CQ. PR= CQ .( AR-AP)
2. En déduire que les droites (CQ) et (PR) sont perpendiculaires.

on n'a aucune valeur donc comment on peut arriver à 0 .
on a pas CQ et RP.

Posté par
dhaltere : exercice produit scalaire 20-02-12 à 20:18

comment ça, tu n'as aucune valeur ?
tu as un carré, donc les cotés ont tous même longueur et tu as des angles droits à foison
tu as un rectangle, encore des angles droits, et des parallèles
AP = DR : c'est pas rien, ça

ton exercice pullule de contraintes largement suffisantes pour faire jouer les propriétés des produits scalaires

exercice produit scalaire

Posté par
lifere 20-02-12 à 20:39

a ok .merci

Posté par
lifere 24-02-12 à 18:24

j'ai essayé de faire l'exercice et j'ai trouvé :

1) CQ.PR= CQ.(AR-AP) car PR=(AR-AP)=(AP-AR)=(PA+AR)=PA ( Chasles )

2) CQ.(AR-AP)= CQ.AR-CQ.AP = CQ.PQ-CQ.RQ  car AR=PQ et AP=RQ et je me suis arrêté la car je ne sais pas comment continuer . j'ai pensé à faire CQ-CQ + PQ.RQ
                              =  0   + QP.QR = 0 car (QP;QR) est droit  . mais je ne croix pas qu'on peut faire comme sa .

Posté par
dhaltere : exercice produit scalaire 24-02-12 à 19:21

on parle de vecteurs :
PR=(AR-AP) : oui
PR=(AR-AP)=(AP-AR) : non

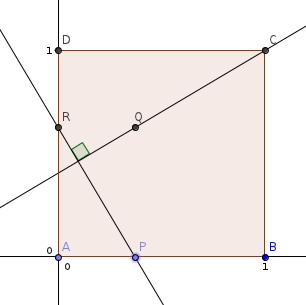
exercice produit scalaire
ABCD carré : on va traduire cela par les propriétés suivantes :
soit a le coté du carré
alors
a²=AB²=||\vec{AB}||²=\vec{AB}²=\vec{AB}.\vec{AB} \\ a²=AD²=||\vec{AD}||²=\vec{AD}²=\vec{AD}.\vec{AD} \\ \vec{AB}.\vec{AD}=0 \\ \vec{DC}=\vec{AB}

en longueurs AP=DR, et P sur le segment [AB], R sur le segment [AD]
Pour traduire cette propriété, nous dirons qu'il existe un réel k tel que
\vec{AP}=k\vec{AB} \\ \vec{DR}=k\vec{DA}

APQR est un rectangle : nous n'aurons besoin que de traduire le fait qu'il s'agit d'un parallélogramme : \vec{AP}=\vec{RQ}

Chasles
\vec{CQ}=\vec{CD}+\vec{DR}+\vec{RQ}

substitution des composantes de cette décomposition
\vec{CQ}=-\vec{AB}+k\vec{DA}+\vec{AP}

\vec{CQ}=(k-1)\vec{AB}-k\vec{AD}

Chasles
\vec{PR}=\vec{PA}+\vec{AD}+\vec{DR}

substitution des composantes de cette décomposition
\vec{PR}=-k\vec{AB}+\vec{AD}+k\vec{DA}

\vec{PR}=-k\vec{AB}+(1-k)\vec{AD}

Donc on résume
\vec{CQ}=(k-1)\vec{AB}-k\vec{AD}
\vec{PR}=-k\vec{AB}+(1-k)\vec{AD}

On effectue maintenant le produit scalaire
\vec{CQ}.\vec{PR}=((k-1)\vec{AB}-k\vec{AD}).(-k\vec{AB}+(1-k)\vec{AD})

On développe en simplifiant les produits scalaires nuls car \vec{AB}.\vec{AD}=0

\vec{CQ}.\vec{PR}=-k(k-1)a²-k(1-k)a²=0

donc les deux droites (CQ) et (PR) sont bien orthogonales

Posté par
lifere 24-02-12 à 21:18

quand tu écris :

CQ=-AB+kDA+AP
CQ=(k-1)AB-kAD ben il n'y a plus "AP" et puis si on développe on va avoir à un moment "kAB" alors que dans la ligne de juste en haut on ne l'a pas .

Posté par
dhaltere : exercice produit scalaire 24-02-12 à 22:40

j'ai remplacé \vec{AP}

cherche un peu comment je suis passé d'une ligne à l'autre.

c'est du calcul mental, mais tu auras peut-être besoin d'une ou même deux étapes intermédiaires.

Posté par
lifere 24-02-12 à 23:31

a oui c'est parec que AP=kAB

Posté par
dhaltere : exercice produit scalaire 25-02-12 à 09:48

tu vois, quand tu te donnes la peine de réfléchir un peu

Posté par
lifere 25-02-12 à 17:42


Rechercher
Menu
Espace membre
19 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1742 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !