Inscription / Connexion Nouveau Sujet
Exercice sur les probabilités conditionnelles
Bonjour à tous, alors voila j'ai un gros problème sur un exercice de probabilité, je n'arrive pas à faire l'arbre pondéré, et sans l'arbre je ne peux pas avancer 
J'espère que quelqu'un saura m'aider à commencer.
Énoncé :
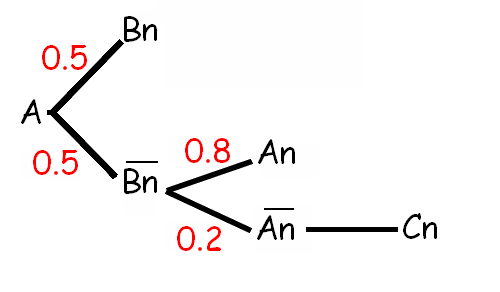
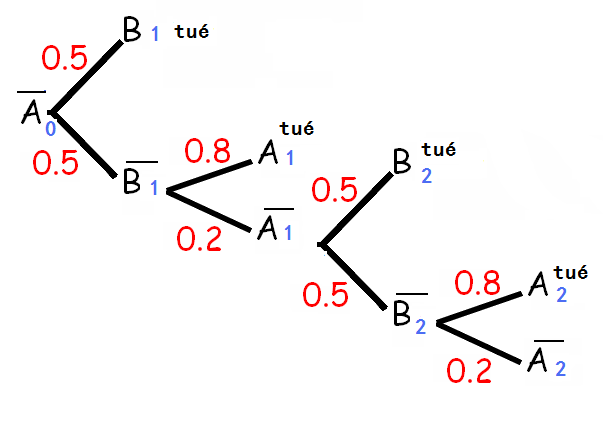
Deux cow-boys A et B se battent en duel. A tire le premier et réussit son tir une fois sur deux. B tire en second avec une réussite de 80%.
Si personne n'est tué, les cow-boys recommencent une nouvelle série de tirs.
On note An : « Le cow-boy A est tué à la nième série de tirs », Bn : « Le cow-boy B est tué à la nième série de tirs » et Cn : « Les deux cow-boys sont vivants après n séries de tirs ». On pose an = p(An ), bn = p(Bn ) et cn = p(Cn ).
1. A l'aide d'un arbre pondéré, calculer a1, b1, et c1.
2.
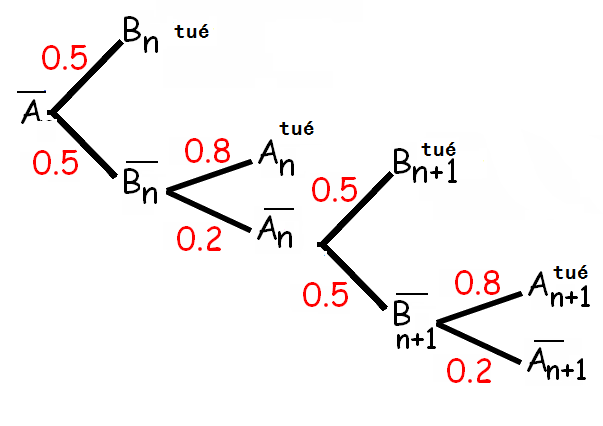
a. Déterminer pCn(Cn+1) et pCñ(Cn+1).
b. En remarquant que p(Cn+1 ) = p(Cr+1 n nCn) + p(Cn+1 n Cñ), montrer que Cn+1 =0,lCn.
etc mais je voudrais juste un coup de pouce pour la première question, vous avez une idée?
Merci à ceux qui répondront 
Bonjour,
dans ton arbre, tu devrais remplacer les "n" par leurs valeurs.
Que signifie pour toi l'événement A1 ? B1 ?
Si je comprends bien, une "série de tirs" c'est quand ils ont tiré tous les deux.
Justement je n'arrive pas à les représenter autrement :s
A1 représente le cow-boy A tué à la 1ère série de tirs et B1 le cow-boy B tué à la 1ère série de tirs également non?
A1 représente le cow-boy A tué à la 1ère série de tirs et B1 le cow-boy B tué à la 1ère série de tirs également non?
Je pense que oui.
Avec l'arbre, on peut calculer facilement a1 et b1
bonjour,
/
/0,5
/
A---------------------------
0,5 \ 0,8
\0,2
\
*A tire le premier et tue B avec une probabilité égale à 0,5 chemin
sinon A rate B chemin avec encore p=0,5
**B étant vivant
il tue A avecp=0,8 chemin
il rate A chemin
donc
Ok, merci beaucoup je ne vous embête plus je vais pouvoir avancer maintenant :p 
Bonne fin de journée à vous et encore merci borneo et veleda. 
Bonjour tout le monde j'ai le même exercice à traiter. L'arbre que vous proposer semble cohérent mais pour trouver les probalitités faisant intervenir Cn c'est difficile car Cn n'aparait pas dans l'arbre. De plus, je ne vois pas comment on peut calculer pCñ(Cn+1)étant donné que si j'ai bien compris Cñ correspond à "les deux cowboys sont morts". S'ils sont morts ils ne pourront plus être vivants après.
Pourriez-vous m'aider s'il vous plait ?
Bonjour,
c'est cette question ?
b. En remarquant que p(Cn+1 ) = p(Cr+1 n nCn) + p(Cn+1 n Cñ), montrer que Cn+1 =0,lCn.
C'est quoi, r ?
a. Déterminer PCn(Cn+1)
Si au nième échange de tirs les deux sont vivants, ils le seront encore après un autre échange (n+1) si aucun des deux n'est tué, c'est le chemin Anbar inter Bnbar = 0.5*0.2
donc PCn(Cn+1) = 0.1
Comme l'a dit Veleda, pCñ(Cn+1) = 0
s'ils ne sont pas vivant à l'instant n, ils ne peuvent pas l'être à n+1
Pour la dernière question, on additionne les deux et on trouve la réponse. Je pense que l'exo est terminé. 
Merci à borneo et à veleda pour votre aide. Cela va me permettre de poursuivre l'exercice qui n'est malheureusement pas terminé  .
.
Grâce à l'abre je vais pouvoir poursuivre merci