Inscription / Connexion Nouveau Sujet
Exercice sur les produits scalaires avec une figure géométrique
Bonsoir, Pourriez-vous m'aider s'il vous plaît pour cette exercice concernant le chapitre les produits scalaires.
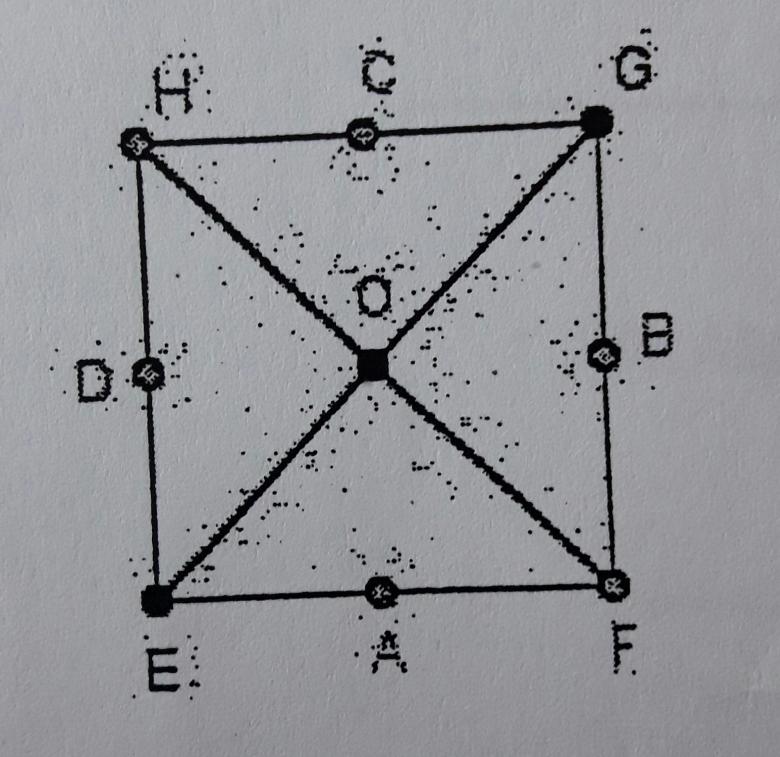
On considère le carré EFGH de coté a ci-dessous :
Dans ce carré, A est le milieu de [EF], B est le milieu de[FG], C est le milieu de [GH], D est le milieu de [HE] et O est le centre de EFGH.
Exprimer en fonction de a les produits scalaires suivants :
1.
2.
3.
4.
5.
6.
7.
Pourriez-vous svp me donner un exemple pour la premier question pour que je puisse voir la façon dont il faut rédiger.
tu connais la longueur HO, la longueur HF (donc les normes de tes deux vecteurs)
l'angle entre tes deux vecteurs, donc son cosinus....
essaie, et recopie qu'on voit
Si j'ai bien compris, faut utiliser la propriété sur les projective
On a donc
u.v = ║u║*║v║*cos(u;v)
HO.HF = HO*HF* cos(u;v)
Mais après je bloque, le problème étant que , sont superposé, donc je ne vois pas comment on pourrait lire l'angle.
On a donc
u.v = ║u║*║v║*cos(u;v)
HO.HF = HO*HF* cos(0)
HO.HF = 1/a*a*cos(0)
C'est le bon raisonnement ?
HO et HF doivent être calculés correctement
et j'espère que tu sais ce que vaut cos(0)
voilà, tu connais la méthode maintenant....
Oui, cos(0) = 1
On a donc
u.v = ║u║*║v║*cos(u;v)
HO.HF = HO*HF* cos(0)
HO.HF = 1/a*a*1
Mais je ne vois pas comment terminer.
C'est bien,
J'utilise l'égalité de Pythagore, donc :
HF^2 = HO^2 + OF^2
BC^2 = (1/a)^2 + (1/a)^2
BC^2 = 2*(1/a)^2
BC^2 = √(2*(1/a)^2)
Mais après je ne vois pas comment poursuivre.
C'est dans le triangle rectangle FEH que tu peux calculer la longueur de HF à l'aide du théorème de Pythagore.
Juste c'est HF², non pas BC.
Donc,
HF² = HE^2 + EF^2
HF² = a² + a²
HF² = 2*a²
HF² = √ (2*a²) = √2 + √a² = √2 + a
On a, HF² = √2 + a
Je ne sais pas si c'est le bon raisonnement.
vecHO.vecHF = |HO|*|HF|cos(vecHO, vecHF)
Or, l'angle (vecHO, vecHF) est nul (cf 21h39). Son cosinus est donc égal à 1.
Ainsi, le produit scalaire des deux vecteurs est égal au produit de leurs longueurs (ou normes).
Du coup, pour appliquer la formule, faudrait également effectuer le théorème de Pythagore pour HO à l'aide de HC et CO, donc HO² = HC^2 + CO^2 ?

 (2a²) =
(2a²) = 
