Inscription / Connexion Nouveau Sujet
Exercice, triangle equilatéral dans carré.
Bonjuor à tous.
J'inaugure mon 1re post sur ce forum en vous demandant de l'aide pour l'un des exercice de mon DM de math de trigonométrie niveau 1re S.
J'ai réalisé notre figure sur paint.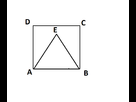
ABCD est un carré direct, ABE est un triangle équilatéral direct.
1\ Calculer les mesure en radian de chacun des angles orientés suivant :
(AB, AE); (BC, BE); (EA, EC)
2\ Calculer les mesure en radian de chacun des angles orientés suivant :
(AD, EC); (DC, EC); (AE, BE)
J'ai trouvé les deux premiers résultats.
Pour AB AE.
Sommes des angles d'un triangle = 
. Et comme celui ci est équilatéral, on a naturellement /3
Pour BC BE.
BC BA = /2 car nous avons un angle droit.
BC BA - BE BA = BC BE/2 - /3 = /6
Je bloque ensuite à celui d après.
EA EC n est d autre que EA EB + EB EC.
On a EA EB, mais je bloque pour trouver EB EC.
... J'ai essayé de decomposer le triangle .. Ca ne m avance pas.
De l'aide serait-possible ? J'ai encore beaucoup de mal en trigonométrie, merci d avance 
Cordialement, KimiLePetit.
A mon avis, on ne peut pas calculer l'angle (EB,EC) sans faire appel à la nature du triangle EBC et aux règles régissant les angles d'un triangle.
Je ne vois pas ce que tu veux dire ... On a pas les mesures des côtés dans cet exercice, c'est entièrement porté sur les angles orientés.
Je vais essayer de voir ce que ça donne si on "allonge" [AE) et [BE)
Donc j ai trouvé la réponse pour EA EC.
C était.
(EA EC) = (EA EB) + (EB, EC)
= /3 + 5/12
= 3/4.
J'ai raisonné avec les triangles isocèles.
Maintenant j ai une question. La suite me demande (AD EC). Mais nous ne connaissons pas leur point d intersection ... Comment raisonner alors ?
(Désolé pour le multipost, je ne trouve pas l'edition.)
Pour ce qui est de la suite. Je ne suis pas sûr du raisonnement à faire.
J'aimerai savoir ce que vous pensez de mes résultats.
(DC, EC)
Je considère alors que (DC, EC) = (CE, CD)
(CE, CD) = (CB, CD) - (CB, CE)
= /2 - 5/12
(CE, CD) = /12
(DC, EC) = /12
(AE, BE)
Pour le dernier, si mon raisonnement est bon, je n'ai pas saisi la difficultée ...
(AE, BE) = (EA, EB) = /3 car c'est un triangle équilatéral ...
Qu'en pensez vous ? Mon raisonnement est-il faut ?
(AD,EC) : si tu traces la hauteur EH du triangle DEC, tu vois que cet angle est égal à l'angle (EH,EC), lequel peut ^etre calculé.
Tout le reste est bon.
Annuler
connectez vous