Inscription / Connexion Nouveau Sujet
Exercices Angles orientés.
Bonjour à tous et bonnes vacances!
Je vous demande de l'aide car notre professeur de Maths nous a donné un tas d'exercice pour les vacances et je ne suis vraiment pas doués pour les angles orientés. J'aimerai vraiment comprendre ce qu'il m'est demandé de faire car nous allons bientôt avoir un devoir dessus, et je galère totalement! 
Pour le premier exercice
Déterminer la mesure principale des angles de mesure -20 / 3 et 50
/ 3 et 50 / 8
/ 8
Deuxième exercice
soit ( ;
; )= -
)= - /9 et (
/9 et ( ;
; )=
)=  /4 . Determiner la mesure principale de (
/4 . Determiner la mesure principale de ( ;
; ), (-
), (- ,
, )et (-
)et (- ;-
;- )
)
Exercice 3
SAchant que cos2 / 5 = (-1 +
/ 5 = (-1 +  5 )/ 4, calculer la valeur exacte de sin 2
5 )/ 4, calculer la valeur exacte de sin 2 /5 . En déduire les valeurs exactes de sin(-2
/5 . En déduire les valeurs exactes de sin(-2 /5) et sin3
/5) et sin3 /5
/5
Exercice 4
Ecrire les égalités suivantes en fonction de cosx et/ou sinx
(voir attaché)
Exercice 5
ABC est un triangle rectangle direct en A, tel que AB=2AC
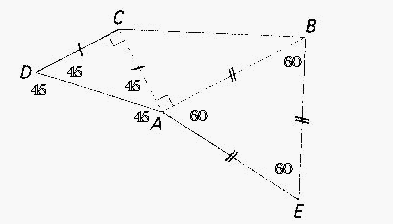
ACD est un triangle direct isocèle et rectangle en C et BAE un triangle équilatéral direct(voir image). Donner en justifiant la mesure principale des angle suivants :
(ce sont tous des vecteur) (AD;AE) (CB;AD) (EA;BC)
Et enfin, exercice 6
Soit la fonction f définie par  (x)= 3x2+ ax + b / x2= 1
(x)= 3x2+ ax + b / x2= 1
Le réel a et b étant à déterminer. On appelle C sa courbe représentative dans un repère orthonormé
1) Quels sont ses ensembles de dérivabilité et de Définition ?
2)Déterminer a et b pour que la tangente à C au point d'abscisse 0 ait pour équation y= 4x + 3
3)Etudier  (x) - (4x+3) et en déduire la position de C par rapport à cette tangente.
(x) - (4x+3) et en déduire la position de C par rapport à cette tangente.
4)Dresser le tableau de variation de f
5)La fonction f admet-elle des extrêmes sur  ? Lesquels ? Justifier la réponse.
? Lesquels ? Justifier la réponse.
6) tracer la courbe représentative de la fonction 
Voila, merci pour toute aide qui est bien entendu la bienvenue !!
bonjour ,
Ouh lala ...
UN topic = UN exo
A la rigueur les 4 premiers concernent les angles orientés, on les traitra ici. Pour l'exercice 6 , copie-colle et ouvre un nouveau sujet .
exercice1:
-20pi/3 = -18pi/3 -2 pi/3
= -6pi -2pi/3
donc la determination principale de -20pi/3 est -2pi/3
fais de meme pour l'autre
exercice 2
ce sont les formules du cours...
exercice 3
pour calculer le sin , utilise: cos²a+sin²a=1
puis sin(-2pi/5) = -sin(2pi/5)
et sin 3pi/5 = sin(pi-2pi/5)
exercice 4
utilise les formules de transformation cos(a+b) , sin (a+b) etc...
je regarde le dernier

bonjour et merci de tes réponses rapides ^^
Je pense avoir compris pour le premier merci !
Mais pour le deuxième, qu'est ce que tu veux dire par les formules du cours? car ns avons pas tous le même cours..
Merci encore!
ton cours donne les formules de calcul avec les angles orientes.
genre:
(u;-v) = (-u;v) = (u;v)+pi
(v;u) = -(u;v)
(-u;-v)= (u;v)

et pour le dernier:
exercice 5
en utilisant les proprietes des triangles isocèles et equilateraux, tu peux placer tes angles:
[img1]
puis Chasles te donne: ( avec des vecteurs bien sûr)
(AD,AE) = (AD,AC)+(AC,AB)+(AB,AE)
reste à trouver la valeur des angles en tenant compte du sens d'orientation du plan.
(AD,AE) = -pi/4 - pi/2 - pi/3 = …
essaie pour les autres!

Donc si j'ai bien compris, pour le 1)
50pi/8 = 48pi/8 + 2pi/8
= 6pi + pi/4
donc la mesure principale est pi/4 ?
voici ce que j'ai trouvé pour la suite !
Exercice 2
(v;w) = 13pi/36
(-u;v) = 8pi/8
(-v;-w)=13pi/36
Exercice 3
sin 2pi/5 =  (10 + 2
(10 + 2 5) / 4
5) / 4
mais je bloque avec sin 3pi/ 5 
Exercice 4
A(x) = -sin(x) - cos(x)
B(x) = O
Exercice 5
(AD;AE) = 13pi/12
et je fais la suite
bonsoir,
exercice 2:
(v;w) = 13pi/36 ---> on te demandait (u,w) et je trouve: 5pi/36
(-u;v) = 8pi/8 ---> euh presque : 8pi/9
(-v;-w)=13pi/36 ---> oki ! 
exercice 3:
sin 2pi/5 = ---> OK
pour sin 3pi/5 tu peux ecrire : sin 3pi/5 = sin ( pi - 2pi/5)
et tu utilises la formule sin(a-b)= ...
exercice 4
laisse moi le temps de calculer A et B pour confirmer 
exercice 5
attention , tu as surement caculé 13pi/12 en passant par l'angle obtus. Tu vas de AD vers AE dans le sens antitrigo donc (AD,AE) = -13pi/12 (ou 11pi/12)

bonsoir,
exercice 2:
(v;w) = 13pi/36 ---> on te demandait (u,w) et je trouve: 5pi/36
(-u;v) = 8pi/8 ---> euh presque : 8pi/9
(-v;-w)=13pi/36 ---> oki !
Dac! en fait je me suis trompé en copiant l'énoncé je suis sincerement désolé! il me demandait en fait (v;w)
exercice 3:
sin 2pi/5 = ---> OK
pour sin 3pi/5 tu peux ecrire : sin 3pi/5 = sin ( pi - 2pi/5)
et tu utilises la formule sin(a-b)= ...
exercice 4
laisse moi le temps de calculer A et B pour confirmer
Ah, je n'ai pas calculé A et B ? o_0
exercice 5
attention , tu as surement calculé 13pi/12 en passant par l'angle obtus. Tu vas de AD vers AE dans le sens antitrigo donc (AD,AE) = -13pi/12 (ou 11pi/12)
Exact! merci !
oui tu avais calculé A et B mais pas moi! 
Bon je trouve 0 pour A comme pour B.
Refais tes calculs , et si besoin je poste le détail( après le repas  )
)
Pour (v,w) , ok pour 13pi/36

En le refaisant je m'aperçois que je n'avais pas pris la bonne formule pour A... 
A = sin(7 /2 - x) + cos(6
/2 - x) + cos(6 +x) + sin(7
+x) + sin(7 +x)+sin(x+
+x)+sin(x+ /2)
/2)
= sin(7 /2).cos x - sin x .cos(7
/2).cos x - sin x .cos(7 /2) + cos x + sin(
/2) + cos x + sin( +x)+ cos x
+x)+ cos x
= -cos x + cos x - sin x + cos x
= cos x - sin x
B = cos(5 /2-x) + cos(2
/2-x) + cos(2 -x)+ cos(7
-x)+ cos(7 -x) + sin(x+
-x) + sin(x+ )
)
= cos( /2-x) + cos x + cos(
/2-x) + cos x + cos( pi-x ) + sin ( x+
pi-x ) + sin ( x+  )
)
= sin x + cos x - cos x - sin x
= 0

Voici ce que je ne trouvais pas pareil pour
Est-ce que l'on peut dire que:
= sin( 4pi/2 + 3pi/2 - x)
= sin ( pi/2 + pi - x) or (sin(pi/2-x) => cos(x)
= cos(pi-x)
=
Moi j'ai exactement les memes exercices et il y a deux trucs que j'arrivent toujours pas 
Au niveau de l'exercice 3 je ne comprend pas du tout coment vous avez fait pour calculer le tout, pourriez vous me montrer les calculs svp?
Et enfin, pour l'exercice 5 je ne voit pas non plus comment vous avez fait de un pour trouver la relation de chasles et de deux pour trouver que c'est -2pi / 4 ect
Comment vous faites pour les angles d'après svp ?
Merci beaucoup davance,
bonjour,
exercice 3:
cos²(2 /5) + sin²(2
/5) + sin²(2 /5) = 1 donc sin²(2
/5) = 1 donc sin²(2 /5) = 1-cos²(2
/5) = 1-cos²(2 /5)
/5)
sin² (2 /5) =
/5) =
ce qui apres calculs donne: sin²(2 /5) =
/5) = et donc sin(2
 /5) =
/5) =
puis:
sin (-2 /5) = -sin(2
/5) = -sin(2 /5) = -
/5) = -
et :
sin(3 /5) = sin (5
/5) = sin (5 /5 - 2
/5 - 2 /5)
/5)
= sin ( -2
-2 /5) or sin(
/5) or sin( +x) = -sinx
+x) = -sinx
= -sin(-2 /5)
/5)
=
c'est bon pour celui ci?

exercice5:
la relation de Chasles s'exprime avec des angles orientés comme tu le faisais avec les vecteurs ( là jette un oeil à ton cours  ) :
) :
Puis sur la figure, les angles géométriques sont placés grâce aux relations d'angles dans les triangles équilatéraux ou isocèles.
Ensuite il faut faire attention au sens lorsque tu lis les angles.
Par exemple:
car on tourne dans les sens contraire au sens trigo quand on passe de
à

Ah enfaite je savait pas comment calculer cos² (2pi/5) c'est pour ça. Mais je comprend mnt pour l'exercice 3.
Par contre l'exercice 5 j'ai toujours rien compris. J'ai reussi a calculer (AD,AE) en faisant ton calcule donné au dessus. Mais je voit pas comment tu trouve que un certain angle = -pi/4 ect
C'est quoi les calculs pour les autres angles: (CB,AD) et (EA,BC) stp ? Peut etre que je verrai mieux comment tu as trouvé.
Merci d'avance,
es tu deja ok avec les angles (45° et 60°) inscrits sur la figure?
On les a déduits des proprietes du triangle CDA isocele en A et ABE equilateral.

Bien ! En radians, 45° donnent  /4 .
/4 .
Quand tu lis l'angle orienté tu passes de
à
en tournant dans les sens contraire au sens trigo. La valeur de l'angle est donc comptée négative.
On a alors:
Toujours d'accord?

Ahhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhh ouai ^^
J'avait trop pas réfléchit à ce que 45° = pi/4
Ca marche je comprend mais tu peux me donner un ptit coup de main pour les relation de chasles Pour les deux autre angles ? j'essairai de trouver combien ça fait 
oK 
Il te reste à trouver la valeur du premier angle en utilisant le fait que ABC est rectangle en A et que ( il y a une erreur dans l'enonce tapé ici)
à toi ! 
L'angle acb = 180 moins l'angle abc
AB = racin CB - Racin AC
AB = Racin 3ac tu le sait comment ?
Aie je suis bloqué oO
Je fait n'importe quoi la non?
C'est plus dur que le premier 
lol oui faut creuser un peu plus! 
en fait ABC est rectangle en A tu peux donc utiliser les formules trigo:
donc
peux tu continuer?

C'est une formule par coeur que quand on a tan racine3, l'angle = Pi / 3 ?
Je continu: (AC,AD) = 90 ° Soit Pi / 2 non? et Pi = 180 ° ?
On a donc (CB, AD) = Pi/ 3 + PI/2 + Pi ?
oui cela fait partie des valeurs à connaitre par coeur 
attention tu as des erreurs:
(CB,CA) = -pi/3
(AC,AD) = pi/4
donc : (CB,AD ) = -pi/3 + pi/4 + pi
= 11pi/12
tu essaies le dernier ?

Ah oui c'est en fonction de la rotation de quel cote on prend l'angle c'est ça ? Si on tourne pas dans le sens direct c'est moins et sinon c'est plus ?
Pour le dernier tu peux me donner la relation de chasles stp ? serait sympas 
ah tu as posté entre temps:
oui c'est juste ce que tu dis.
pour le dernier: ( je te mets le vecteur en rouge pour te montrer comment je le construis)
je continue sans les vecteurs pour ecrire plus vite:
= (-AE;-AB) + (BA;BC)
= (AE;AB) + (BA;BC)
à toi !
(tu dois trouver pi/6)

Donc on a PI/ 3 - (AC/BA)Car on tourne dans le sens inverse et que on utilise la tangent c'est ça ?
Mais ça fait combien AC/BA en PI stp ?
Dernière question promis aprs je trouve solo 
Merci de ton aide,
euh...
je ne comprends pas ce que tu as ecrit là: PI/ 3 - (AC/BA) ???
tu ne peux pas donner l'angle (AC,BA)directement il faudrait que les deux vecteurs aient la meme origine genre (AC,AB).
Mais de toute façon on n'en a pas besoin ici .
(AE,AB) = pi/3 (sens direct)
(BA,BC) = ?
geometriquement BAC est le complementaire de ACB et vaut donc pi/6
on tourne dans le sens anti-trigo donc (BA,BC) = -pi/6
d'òu :
(EA,BC) = pi/3 - pi/6
= pi/6
ok?

ah ouai, non j'ete en train de calculer la tangente de (ba, bc) XD avec la trigonométrie
Mais encore merci bcp, je te dirais comment ça s'est passé et si c'est tous juste un peu bcp grace a toi  )
)
Encore merci beaucoup,