Inscription / Connexion Nouveau Sujet
Exercices Dérivation
Bonjour,
J'ai un dm sur les tangentes et les nombres dérivés mais je bloque a la question 2 pouvez vous m'aider svp. A la question 1 je trouve 7/5 est-ce correct ?
Voici l'énoncé :
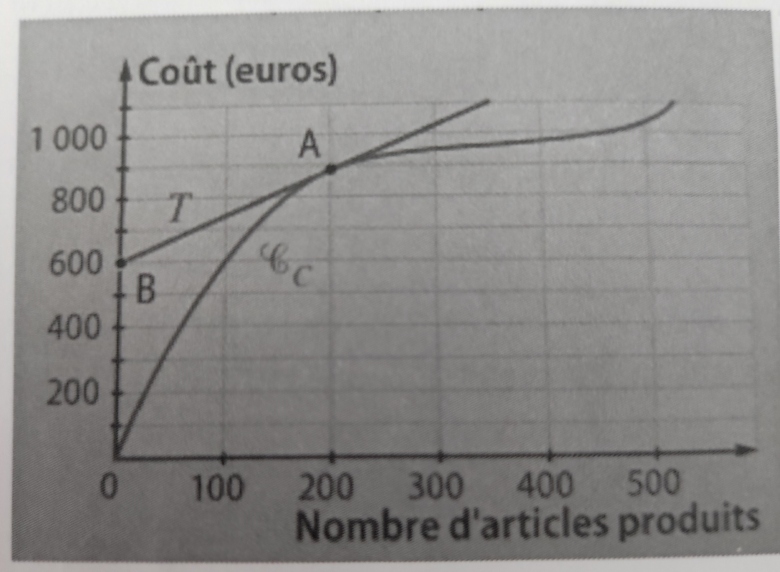
L'entreprise Sportymax fabrique des articles de sport. Le coût total de ces articles (en euros) est modélisé par une fonction C, dont la courbe représentative Cc est donnée ci-dessous.
La tangente Ta à cette courbe au point A(200;880) passe par le point B(0;600).
1) On appelle coût marginal au rang n le coût engendré par la fabrication du n ème article. Une valeur approchée de ce coût marginal est donnée par le nombre dérivé de la fonction coût en n.
Déterminer le coût marginal au rang 200.
2) Expliquer la démarche à réaliser graphi quement pour déterminer le coût margi nal le plus faible.
Graphique en pièce jointe
Bonjour,
1) Ton résultat n'est pas correct.
Le nombre dérivé au point est la pente (ou coefficient directeur) de la droite
.
J'ai pourtant bien calculé le coefficient directeur de la droite (AB)
Y = MX + P
M = YB - YA / XB - XA
Mince ! Tu as raison. J'avais pris graphiquement l'ordonnée de A :900 alors que le texte indique 880.
Désolé !
Pour 2) on te parle de méthode graphique : le coût marginal sera minimum au point de la courbe où sa tangente aura un coefficient directeur minimum.
Tu déplaces virtuellement le point et la tangente correspondante sur la courbe.
Tu dois situer approximativement le point de cette courbe où la tangente a un coefficient directeur minimum. Autrement dit, le point où la tangente en question est la plus proche de "l'horizontale".
A peu près; je dirais aux alentours de 350.
Sur , le coefficient directeur diminue autrement dit
est décroissante.
Sur, le coefficient directeur augmente autrement dit
est croissante.
passe par un minimum pour
Pour information le point de la courbe d'abscisse est appelé "point d'inflexion.



