Inscription / Connexion Nouveau Sujet
exo dérivée 1ere s
Voila voila j'ai un exo à faire et j'suis pas sûre de moi !
voici l'énoncé :
On considère les courbes C1, C2, C3, d'équation respectives :
y=-x²+3x+6
y=x²+7x+8
y=xcube-x²+4
a)Démontrer qu'il existe un point commun A aux courbes C1, C2 et C3.
b)Ces courbes admettent-elles la même tangente en A ?
Alors moi j'ai commencé à dire que pour qu'un point soient comuns aux trois courbes il faut que que ses coordonnées vérifient l'équation de chaque courbe et donc soit solution du système:
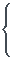y=-x²+3x+6 (1)
y=x²+7x+8 (2)
y=xcube-x²+4 (3)
(1) et (2) donnent :
-x²+3x+6=x²+7x+8
2x²+4x+2=0
(
2 x+2)²=0
2 x+2=0
d'où x=-1
C1 et C2 ont un point comun d'abssice -1
Soit A ce point
yA=-(1)²+3x(-1)+6
yA=2
A(-1;2)
ensuite c'est là où j'ai un problème, est ce que je peux remplacer les coordonnées de ce point dans la 3ème équation et voir si ça marche? (en + ça marche alors ça m'arrangerait!)
merci bien!
Bonsoir sarah29,
ta démarche est la bonne (j'ai pas vérifier les calculs) mais si tu as trouvé un point commun à C1 et C2 et que tu remplaces dans l'équation de la courbe C3 les x et y par les coordonnées de ce point et qu'effectivement l'équation est vérifiée alors c'est que c'est bien un point de C3 et donc tu as gagné.
Pour ce qui est de la tangente, il te suffit de calculer la dérivée en l'abscisse du point A pour chacune des fonctions représentées par C1, C2 et C3 (cela te donnera le coefficient directeur de chacune des tangentes et comme elle passe par A si ces dérivées sont les mêmes en cet abscisse les tangentes sont les mêmes car cette tangente est alors la droite passant par A et de vecteur directeur d'abscisse 1 et d'ordonnées la dérivée à l'abscisse du point A ce qui définit bien une unique droite).
Salut 
Annuler
connectez vous