Bonjour,

il faut traduire la condition" (AI) perpendiculaire à (BD)" en une équation faisant intervenir a

la méthode est dans cet exo totalement au choix (à ton choix) :
produit scalaire, ou coordonnées dans un repère au choix (qui doit être orthonormé pour parler d'angles droits), ou angles égaux à traduire en relations trigo etc.

chacune de ces méthode aboutit
à toi de choisir...

Bonjour karl123,
relis ton énoncé, ne vois-tu pas une chose importante qui manque ?

c'est vrai que "On note ke milieu DC" est assez ésotérique
mais bon relecture et réactivité ne sont pas le lot commun chez les demandeurs de nos jours...
(mais vu l'heure du post, il doit y avoir un décalage de fuseaux horaires ... les réactions de même par conséquent)

grr marre de cette liaison Internet.

on note le mileu DC, desole pour la faute...

il y a un bouton Aperçu qui force une relecture plus efficace que de relire simplement ce qu'on est en train de taper (relecture par l'oeil au lieu de relecture "par la main qui tape")

mais le fond du problème n'est pas là

que choisis tu comme méthode
je t'en ai cité plusieurs.

On note I le milieu de DC*

je bloque, car je ne sais pas la valeur du point I, qui est de toute maniere milieu de DC et qui du coup depend de petit a, puisque comme c'est un rectangle AB//DC

je ne sais pas quoi donner comme valeur au point I*

la valeur d'un point ça n'existe pas
exprime toi correctement
ce sera les coordonnées du point (dans un repère à définir précisément avant)
ou bien la mesure de [CI] : CI = a/2
etc

de toute façon ne cherches pas de valeurs numérique avant la fin de l'exo (avant de les avoir trouvées, ce serait absurde si on les connaissait avant, il n'y aurait même pas d'exo !!)

a s'écrit a et c'est tout
et tous les calculs se font en littéral avec partout où intervient la mesure de [AB] ou de [CD] a écrit a etc

Je pense que pour definir quelles sont la valeurs de a lorsque AI est perpendiculaire à DB, il  faut utiliser pythagore soit

AI*2=AD*2 + DI*2
AI*2=1*2+DI*2

et que du coup la valeur de a influe sur l'angle ADC, et que pour que les droites soient perpendiculaires, la droite BD doit passer par D de facon à ce qu'on obtienne

AOB = 45 degre
et
IOB = 45 degre

ensuite je bloque

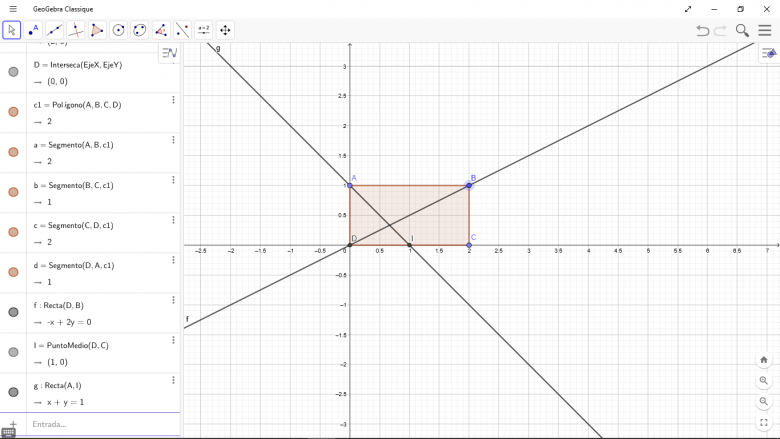
Figure obligatoire avant d'écrire de telles âneries.



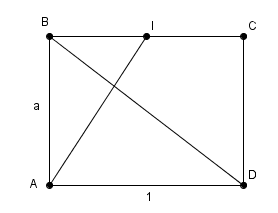
AI*2=AD*2 + DI*2

cela traduit que le triangle AID serait rectangle en D !!!
bein voyons, aucun rapport avec AI et BD perpendiculaires !
et même que ça ne risque pas d'arriver que AD et DI seraient perpendiculaires vu que I ne peut pas être sur la droite (CD) !!

et
la droite BD doit passer par D

beh oui la droite (BD) passe forcément par D quoi qu'il arrive vu que c'est la définition d'une droite (BD) de passer par B et par D !!

quant à tes angles de 45° tu rêves.

arrêtons ces délires et reprenons correctement

choix d'une méthode :
et je ne t'ai pas parlé de Pythagore parce que ça conduirait à des calculs abominables
et ce avant d'inventer quelque valeur ou relation rêvée que ce soit.

je n'avais pas vu ta figure
de toute façon illisible (copie d'écran drap de lit, et des tas de trucs inutiles dedans, réduite par le site donc caractères à s'esquinter les yeux)
mais ça ne change rigoureusement rien à ce que j'ai dit.

ok je crois que j'ai compris, du couo en effectuant Chasles, on obtient :

AI = AB +BI
BD = BA + AD

et du coup on a comme coordonnées du vecteur :

AI = (a;1/2)
BD = (a/1)

et il ne nous reste plus qu'a appliquer la formule pour prouver que ces vecteurs soient orthogonaux
est-ce ca ?  

• des coordonnées nécessitent obligatoirement d'avoir défini le repère de façon précise et explicite AVANT
sinon ça ne veut rigoureusement rien dire du tout

• je ne t'ai pas parlé de coordonnées dans la méthode choisie, c'est une AUTRE METHODE,
et dans le calcul de produit scalaire avec Chasles ça n'a pas son mot çà dire dedans !!
et donc il n'y a aucune "formule" à appliquer !!

AI = AB +BI
BD = BA + AD

AI.BD = (AB +BI).(BA + AD)
développer
et calculer chaque produit scalaire dans le développement en tenant comite des vecteurs qui sont orthogonaux (dans le rectangle lui-même, produits scalaires nuls) et de ceux qui sont colinéaires (produits scalaires = ± produit des longueurs, selon qu'ils sont de même sens ou de sens contraire)

c'est CA le calcul qu'on a commencé

pas des coordonnées !

maintenant si tu préfères une autre méthode et faire des calculs de coordonnées, Chasles n'a pas grand chose à voir là dedans !!
et il faut de toute façon définir le repère choisi AVANT.

du coup
AI=AB+BI=a+1/2
BD=BA+AD=a+1

AI*AD=(a+1/2)(a+1)
              =2a+a+1/2a+1/2
              =3,5a + 1/2

est-ce correcte ?

c'est complètement faux
déja il est absolument indispensable de distinguer à l'écriture un vecteur de sa longueur (norme)

soi en écrivant en LaTex
soit AI en écrivant explicitement les mots "en vecteurs"
soit vAI pour le vecteur

n'a aucun rapport avec AI sans rien du tout qui veut dire la mesure du segment [AI]

AI=AB+BI=a+1/2 est complètement absurde
si c'est des longueurs ça se calculerait par pythagore (il est évident que la longueur de AI est inférieure à la somme des longueurs des côtés de l'angle droit !!)

si c'est des vecteurs c'est absurde parce que un vecteur n'est pas un nombre. un vecteur n'a pas de "valeur", le vecteur AB () ne vaut pas "a".

en vecteurs AI = AB+BI reste écrit AB+BI (tout étant des vecteurs) et c'est tout
point barre ce n'est pas du tout égal à une somme de nombres a et1/2 !!

la suite est la continuation directe de cette absurdité initiale

je t'impose de tout écrire en LaTeX, na !! tu seras forcé de distinguer de

en utilisant l'éditeur LaTeX de l'ile ("aide à l'écriture LaTeX", ne pas oublier le bouton Aperçu) pour écrire







de cette façon là
et de développer ce produit scalaire de vecteurs.

etc

seulement une fois développé on aura par exemple un
ces deux vecteurs sont colinéaires et de sens contraires (vu que ils sont même carrément opposés !)
donc leur produit scalaire est l'opposé du produit de leur normes



et du même genre pour tous les produits scalaires dans le développement , en suivant les règles de calculs des produits scalaires

desole je suis perdu je ne comprend rien

résumé :

tu ne sais pas développer ??

c'est des vecteurs ça reste des vecteurs en développant
tu ne peux pas remplacer ça par des valeurs !

ensuite une fois développé tu pourras calculer certains des produits scalaires du développement par les règles de calcul déja rappelées