Inscription / Connexion Nouveau Sujet
Extremum d'une fonction
J'ai un exo a faire pour demain en maths mais je ne comprends pas ..
Si quelqu'un pourrait m'aider ça serait gentil de sa part. Merci d'avance ^^
Donc voila l'exercice :
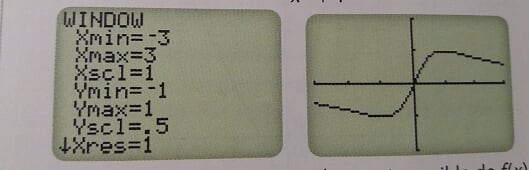
On a représenté sur l'écran de la calculatrice la fonction f définie sur R par : f(x) = x/x²+1
1. Conjecturer le meilleur encadrement possible de f(x) lorsque x est un réel quelconque.
2. Démontrer le résultat conjecturé à la question n°1 (on pourra étudier les variations de la fonction f)
Bonjour
tout d'abord quand on remplace une barre de fraction par une opération de division '/', ajouter des parenthèses obligatoires pour tenir compte de la priorité des opérations, comme vu dans le cours de 5ème
x/x²+1 la division est prioritaire sur l'addition, on effectue la division de x par x² d'abord, puis on ajoute 1
ce qui n'est certainement pas ce que tu as dans ton énoncé (vu que x/x² =1/x !)
s'écrit x/(x²+1)
parenthèses ajoutées absolument obligatoires
et ceci est valable tout au long des calculs que tu feras dans la résolution de l'exo.
la question 1 c'est regarder sur l'écran de ta calculette (ou sur l'image fournie avec l'énoncé) et répondre :
"il me semble que ..." c'est cela conjecturer.
2) faire ce qui est dit : étudier les variations de la fonction...
Ah oui, effectivement j'avais oublié de mettre la courbe et les indications
Et je ne comprends vraiment pas du coup j'ai pas fait grand chose ...
Voici les indications donnée :