Inscription / Connexion Nouveau Sujet
fonction
bonjour je bloque un peu sur cet exercice
soit la fonction f définie pour tout x E R -{-2;2} par f(x) =(-x²+4x)/(x²-9)
1.a déterminer le signe de f(x) pour x E R -{-2;2} (il faut déterminer le signe du numérateur et du dénominateur)
b.Calculer les limites de f aux bornes des intervalles de son ensemble de définition
voila si vous pouviez m'aider merci d'avance!!
Où es-tu perdue ?
As-tu fais le tableau montrant le signe de f(x) en fonction de x ?
Puisque tu as 2 valeurs interdites : 3 et -3, il est normale d'avoir 2 asymptotes verticales d'équation x = 3 et x = -3 .... non ?
oui c'est ça d'accord ça c'est bon mais pour les limites il faut que j'étudie la fonction en + -oo en 3 et en -3??
pour le tableau, tu mets dans la colonne de gauche:
x
-x+4
x+3
x-3
et tu calcules leurs signes entre - et -3, puis de -3 à 0, puis de 0 à 3, puis de 3 à 4, puis de 4 à +
et -3, puis de -3 à 0, puis de 0 à 3, puis de 3 à 4, puis de 4 à +
tu en déduis la valeur de f(x) dans chaque intervalle
tu vas trouver le signe de f(x): - puis + puis - puis + puis -
toutes les valeurs de f(x) en fonction de x te sont données dans le schéma de Raymond (cf plus haut)
Dernière chose:
as-tu remarqué que f(x) tend vers une asymptote d'équation y = -1 qd x tend vers - ou +
ou + ?
?
non en quoi cela peut -il nous aidé?
au fait pour le graphique j'aimerai avec quel logiciel raymond l'a fait parce que ce logiciel trace la corube lorsque x=3 et -3 tandis que le mien non
si tu calcules f(x) quand x tend vers - tu écris:
tu écris:
f(x) = [x2(-1 + 4/x)]/[x2(1-9/x2)]
= (-1 + 4/x)/(1-9/x2)
or 4/x = 0 et 9/x2 = 0 qd x = -
donc f(x) = -1/1 = -1 (asymptote horizontale)

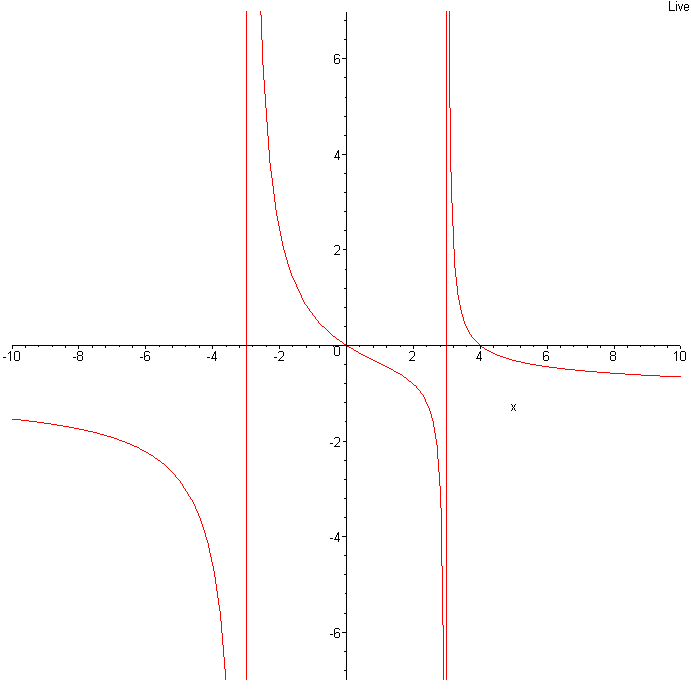

 - {-3;3} ?
- {-3;3} ? -
-

