Inscription / Connexion Nouveau Sujet
Fonction
Bonjour à vous!
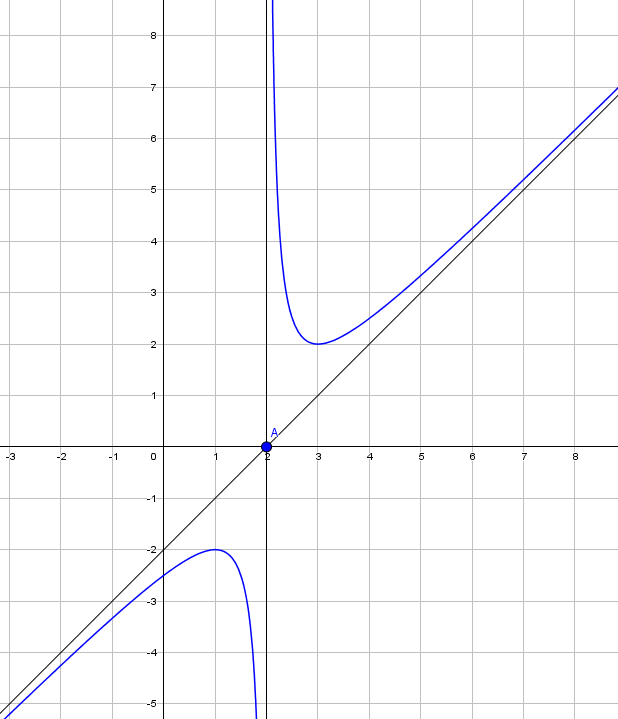
On donne ci-contre une partie de la fonction rationnelle g qui admet le point À (2;0) comme centre de symétrie.
1 ) déterminer l'ensemble de définition D de la fonction g.
2 ) Déterminer graphiquement les limites de la fonction g en 2+ et en +
3) justifier que g(x)=-g(4-x) pour x D , 4-x
D , 4-x D
D
4) en déduire que g(1) = -2 et que g(0) = -2,5
5) reproduire la figure ci-contre et compléter la courbe de la fonction g.
Le problème je peux pas schématiser la figure mais voilà les indications :
Dans un repère orthonorme 2 représente l'asymptote verticale et le point -2 sur l'axe de ordonnée et 2 sur l'axe des abscisses représente l'asymptote oblique le point 3 sur l'axe des abscisses et 2 sur l'axe de ordonnée forme une demi-tangente la partie de la courbe qu'ils sont donné commence de + et décroît sur la demi-tangante pour remonter jusqu'à +
et décroît sur la demi-tangante pour remonter jusqu'à +
Ce que j'ai fait
1 Dg= [ 2;+ [
[
2 limg(x) = +
x +
+
limg(x)
x 2+=+
2+=+
3 ) j'ai pas put faire
4) j'ai en déduit graphiquement
5 ) pour compléter la courbe j'ai d'abord tracer la deuxième demi-tangente 1 sur l'axe des abscisses et -2 sur l'axe des ordonnées pour tracer jai commence de - jusqu'à la demi-tangente pour redescendre jusqu'à -
jusqu'à la demi-tangente pour redescendre jusqu'à -
Oui mais la courbe du bas n'apparaît pas uniquement celle du haut c'est la question 5 qu'on demande de compléter
sinon la fonction ne peut admettre un centre de symétrie
3) que vaut pour
Comment définissez-vous le centre de symétrie ?
Notion de centre de symétrie voilà
g(2+X)+g(2-X)=2x0
g(2+X)+g(2-X)=0
g(2-X)=-g(2+X)
Posons X=2-x
g(2-2+x)=-g(2+2-x)
g(x)=-g(4-x)
Voilà 😎
Si vous voulez sauf que le symbole de la multiplication est :
à défaut * ou .
Une liste de symbole dans en dessous de la feuille de réponse.
pour 4) Que faites-vous ?
Oui, mais si c'est un autre exercice sans rapport avec icelui, il faut ouvrir un nouveau sujet.
De rien
A la question 4 je sais que c'est la notion d'image j'ai lu graphiquement bon comme ils sont demandés d'enduire je sais pas s'il y'a une méthode pour ça