Inscription / Connexion Nouveau Sujet
fonction cube
Bonjour/Bonsoir,
Mon DM de mathématiques me pose quelques problèmes.
Pourriez-vous m'aider s'il vous plaît ?
Vos remarques sont les bienvenues.
Voici le sujet :
Soit la fonction f définie par f(x) = 2x3 - 9x2 + 12x - 4,5
a) Etudier les variations de f
b) Préciser les extrema de f, s'ils sont locaux ou globaux. Dans le cas d'un extremum local préciser un intervalle sur lequel la fonction admet un extremum local.
c) Représenter f graphiquement.
d) Démontrer que l'équation f(x)= 0 admet trois solutions et donner des intervalles d'encadrement de ces solutions.(on donnera à chaque fois un intervalle dans lequel se trouve une solution et une seule. Remarque : on ne demande pas d'expliciter ces solutions).
Voici mes réponses :
a) f(x)= 2x3-9x2+12x-4,5
f'(x)= 6x2-18x+12
= -182-(4*6*12)
= 314-228
= 86
> 0
x1= (18-
86)/12 
O,8
x2= (18+86)/12 2,4
f croissante sur ]-
; (18-86)/12[
](18+86)/12; + [
f décroissante sur ](18-86)/12; (18+86)/12[
b) Si la dérivée s'annule en x0 en changeant de signe alors le point (x0; f(x0)) est un extremum local.
Donc d'après le tableau de variation précédent les extrema locaux sont x1 et x2.
Le maximum local est atteint en (x1; f(x1))
Le minimum local est atteint en (x2; f(x2))
Or on s'aperçoit que ce snt les seuls extrema de f sur 
donc ce sont des extrema globaux.
c) tracer la fonction
d) Avec f(0)= -4,5
f(3)= 4,5
Sur ]-; x1[
f est continue et dérivable
f est croissante
0 
]-; f(x1)[
0 ]-4,5 ; +[
Sur ]x2;+[
f est continue et dérivable
f est croissante
0 ]f(x2);+[
0 ]f(x2); 4,5[
Sur ]x1;x2[
f est continue et dérivable
f est décrissante
0 ]f(x1); f(x2)[
Donc d'après le corollaire du théorème des valeurs intermédiaires f(x)=0 admet trois solutions sur
Recalcule ton discriminant pour la dérivée = 0
Tu devrais trouver 36 au lieu de 86 ...
Et cela rend alors les choses plus facile.
OUUUUUUPPPSSSSS !!! ^^''''
Bonjour/ Bonsoir à tous.
Merci beaucoup pour vos réponses et surtout d'avoir remarqué mes fautes (hemm ^^'''')
Du coup, ça me donne :
a) = 182-(4*6*12)
= 324 - 288
= 36
>0
(36)= 6
x1= (18-6)/12 = 1
x2= (18+6)/12 = 2
(ça c'est sur, c'est beaucoup plus simple tout d'un coup ^^ wahou, merci !!!! ^^')
Les réponses suivantes restent les mêmes, mais je ne fais que remplacer (je mets les bonnes réponses au lieu de mes erreurs)
f croissante sur ]-; 1[]2; +[
f décroissante sur ]1; 2[
b) Mêmes réponses que précedemment, ça ne change pas.
c) tracer la fonction (ça... ça me parraît un peu compliqué ici... mais j'ai l'aspect général, tout va bien ^^)
d) Pareil ^^
Wahouuuu !
Ah ben c'est sur, là, c'est plus simple ^^... Au lieu de taper des x1 ou/ et x2 pour remplacer les x de ma fonction, 1 et 2, c'est tout de même moins fastidieux ^^'
Merci beaucoup de m'avoir aidé ^^ C'est vraiment super gentil. Merci 
Bonsoir!
Ainsi tu peux remplacer à la question d) par les valeurs réels de f(x1) et f(x2) qui sont maintenant simple à calculer (il faut laisser tes calculs sur ta copie pour que ton professeur sache d'où viennent tes résultats)
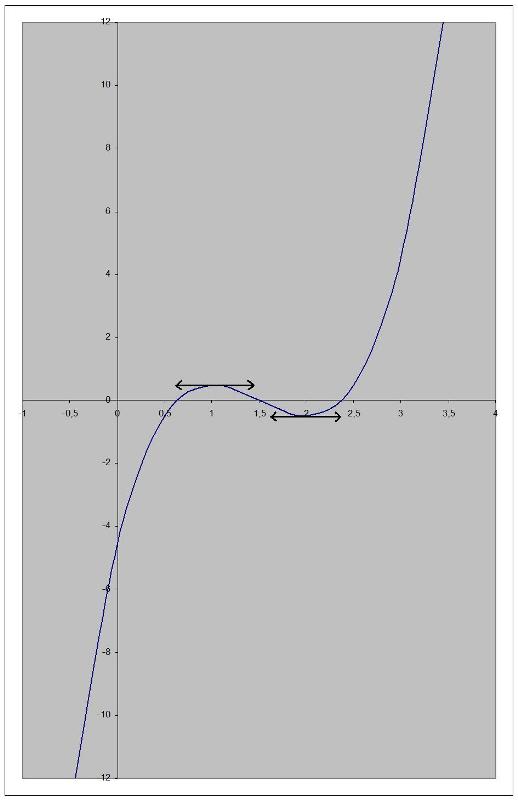
Pour le tracer ne te prend pas la tête: il faudra faire apparaître tes extremums (voir graph). Là par exemple tu pourras tracer ta fonction sur l'intervalle [-1,4] avec 2 cm pour unité graphique. Ensuite pour avoir un beau tracé tu peux utiliser la technique du points par points à l'aide de la fonction "table" de ta calculatrice tous les 0,5!
Bon courage ^^" et bonne soirée!
Annuler
connectez vous