Inscription / Connexion Nouveau Sujet
Fonction d'un graphique en dent de scie
Bonjour,
Ce serait gentil si quelqu'un pouvait m'aider dans la résolution d'un exercice.
L'énoncé comprend un graphique avec les repères (-4,5), (-2,0), (0,5), (2,0) (4,5), ce qui donne un graphique en dents de scie.
"Vous pouvez définir la fonction f représentée en décomposant R en quatre intervalles et un exprimant f(x) sur chacun de ces intervalles, mais essayez de trouver une expression unique valable pour tout nombre x".
Je n'ai pas eu de mal à trouver les fonctions pour chacun des intervalles, à savoir (-5/2x -5); (5/2x + 5); (-5/2x + 5) et (5/2x - 5)
Mais je ne vois pas du tout comment trouver une fonction unique.
Merci pour votre aide
salut, je serais tente de chercher une fonction polynome paire de degre 4.
soit f(x)=a*x^4+b*x^2+c etc ...
Bonjour,
cela me semble hors de propos ici car la courbe serait une fonction "lisse" et pas une fonction définie par morceaux sous forme de segments de droite (ce qui semble ressortir de l'énoncé)
l'astuce consiste à utiliser les propriétés de la fonction valeur absolue.
(x-a) - |x-a| vaut 0 si x > a et 2(x-a) si x < a
en combinant judicieusement les m|x-a| pour les différents points de contrôle on arrive à faire l'exo...
Merci pour ces infos.
Je pensais aussi aux valeurs absolues, mais sans trouver la formule adéquate.
Quant à la fonction polynôme, ça dépasse de loin mes connaissances et je ferais donc l'impasse.
ce n'est pas l'impasse ou pas, c'est que le polynôme ne pourra donner que la courbe en rouge, pas celle en bleu :
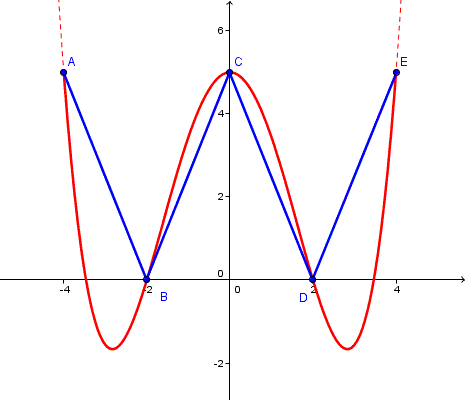
donc le choix est tout vu : prendre ce qui est demandé 
Alors, voilà ce que j'ai trouvé.
f(x) = ||x|-2| * 5/2
Sauf erreur, les images correspondent.
Est-ce que ce serait la solution ?
Merci pour une confirmation
ça m'a l'air tout à fait bon
en profitant "lâchement" ici de la symétrie de la fonction par rapport à l'axe des ordonnées pour éviter des sommes de tout un tas de valeurs absolues.
bien vu.



