Bonjour à tous
Je suis actuellement bloquée sur un devoir de maths que je dois rendre pour dans moins d'une semaine. Le voici:

Dans un cadre économique, on appelle f la fonction de satisfaction une fonction à valeurs dans l'intervalle (0;100). On dit qu'il y a saturation lorsque la satisfaction est à son maximale, c'est à dire lorsque la satisfaction prend sa valeur maximale: 100.
On définit aussi la fonction envie notée v, la dérivée de la fonction satisfaction: v=f'.
Vocabulaire: on dit qu'il y a envie lorsque v est positive, sinon il y a rejet.

Pour chaque partie, on teste un modèle de fonction de satisfaction f.

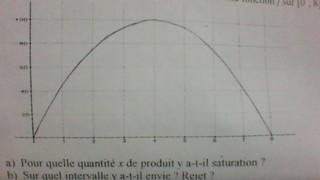
Partie A: Voici l'allure de la courbe représentative d'une fonction f sur (0;8):

(se rapporter au graphique en bas de page)

1 a) Pour quelle quantité x de produit y a-t-il saturation ?
  b) Sur quel intervalle y a-t-il envie ? Rejet ?

2 a)Par lecture graphique donner f(4), puis v(4)
  b) Exprimer v(x) en fonction de x, sachant que v est une fonction affine.

Partie B: La fonction de satisfaction f pour un salaire dans une entreprise est modélisée pour x0 par: f(x)=100x/x+1 où x représente le salaire annuel en milliers d'euros.

a)Déterminer la fonction envie correspondante.
b)Etudier les variations de f pour x0. Tracer l'allure de la courbe de f sur (0;100).
c)A l'aide du tableau de valeurs de la calculatrice, comparer les variations relatives de f pour un salaire passant de 20 00€ à 21 000€ puis pour un salaire passant de 100 000 à 101 000€.
d) Y a-t-il saturation ?
e) Interpréter les résultats obtenus en terme de satisfaction.

Voici ce que j'ai déjà fait:

Partie A
1 a) Il y a saturation pour x = 4.
  b) La dérivée est positive si la fonction est croissante, il y donc envie sur l'intervalle (0;4). La dérivée étant négative si la fonction est décroissante, il y a rejet sur l'intervalle (4;8).

2 a) Par lecture graphique, f(4)=100 et v(4)=0
  b) f est de la forme u/v avec:
u = 100x
v = x+1
u' = 100
v' = 1
Je sais que f'(x)= u'v - uv'/ v²
                 = 100*(x+1)-100x*1/(x+1)²
                 = 100x+100-100x/(x+1)²
                 = 100/(x+1)²
La fonction envie v est égale à la dérivée de la fonction satisfaction f.
Donc v(x)= 100/(x+1)²

Et c'est pour la suite que je suis bloquée...
Pourriez-vous donc me dire dans un premier temps si mes réponses sont exactes, puis m'aider pour la suite, car je ne vois pas du tout comment faire.
Merci d'avance pour le temps que vous prendrez