Bonjour

Ca démarre bien. Comme g est croissante, pour 0[. Comme h'(x)=-g(x), h' est négative donc h est décroissante. A nouveau tu as h(0)=0, donc h est négative.

merci, donc tou mon raisonnement est juste pour l'instant?
la suite:
3.prouver que pour tout réel x strictement positif on a : 0 ≤ x-sin(x)≤ x^3/6

Elle est déjà contenue dans ce que l'on a fait...

oui , mai pour trouver cette question il me manque une information, qui est dans la questio 1 pour déterminer les variation de x-x^3/6-sin(x)
dérrivé h''(x)=sin(x)-x !!
merci de m'aider

SVP:?

bonsoir,

h(x)= x-x^3/6-sin(x)

Etudier les variations et déterminer les signe sur [0;+8[.

j'ai dérivé h(x), h''(x)=sin(x)-x

Ensuite pour les variation ??? merci

*** message déplacé ***

Bonjour,

Ta dérivée seconde est juste.

Tu dois pouvoir démontrer que :
si x>0 alors h"(x)<0
si x<0 alors h"(x)>0
et h"(0)=0

Le signe de h" doit te permettre de connaître le sens de variation de h' :
sur l'intervalle ]-;0] h' est croissante,
sur l'intervalle [0; +[ h' est décroissante.

Tu calcules alors h'(0) qui est le maximum de h'
Tu en déduis le signe de h'
Tu en déduis le sens de variation de h...



*** message déplacé ***

merci baucoup!!!donc je note :

si x>0, alors h''(x)>0  et x<0, alors h''(x)<0
              sinx-x>0                sinx-x<0

Et donc ,h''(0)=sin(0)*0=0*0=00.

donc , comme h'' est positif sur [0;+8[, h' est croissant sur [0;+8[ et inversement pour h'' étant négatif...

h'(o)=1-0²/2-cos(0)=1-0-1=0 étane le max de h',
h' est , je na vois pas pour le signe DESOLE..

          

*** message déplacé ***

aidez moi SVP

*** message déplacé ***

POuvez vous m'aider SVP ??

comment démontrer que
h''(x)=sin(x)-x
si x>0 alors h"(x)<0
si x<0 alors h"(x)>0
et h"(0)=0?

et que pour h'(x)=1-x²/2-cos(x)

si x>0 , alors h'(x)<o
si x<0 , alors h'(x)<o

merci d'avance

merci de me répondre,

désolé je vien de voir ma faute j'ai confudu les signes < et >.
j'ai tout compris!

est-ce que vous pouvez m'aider pour la suite?

3.prouver que pour tout réel x strictement positif on a : 0 ≤ x-sin(x)≤ x^3/6

*** message déplacé ***

voici l'exercice complex qu'on ma donné:
On considère le fonction numérique f de la avriable rééelle x définie sur [o;+8[par:

f(x)=sin(x)/x si x>o
f(o)=1

1.etudier les variations des fonctions de g et h définies sur l'ensemble des réels repectivement par:


g(x)=x-sin(x) et h(x)=x-x^3/6-sin(x)

2. Déterminer le signe de ces deux fonctions sur [o;+8[


j'ai déjà répondu à:

1. variation de g(x):

g'(x)=1-cos(x)
cos(x) étant définie sur [-1;1], 1-cos(x)<0 et donc cos(x)<1 ,donc g'(x) et positif et g(x) et croissant

Variation de h(x)

h'(x)=1-x²/2-cos(x)

h''(x)=sin(x)-x

h'''(x)=cos(x)-1

H(x) est  décroissante sur R.

3.prouver que  pour tout x réel positif on a : 0<= x-sin(x)<= x^3/6

*** message déplacé ***

Bonjour,

(1) On sait que si x>0, alors h"(x)<0, donc -x+sin(x)<0 donc 0<x-sin(x) d'une part ...

et, puisque h est décroissante sur R et que h(0)=0, on peut dire que
(2) si x>0 alors h(x)<0 donc x-x³/6-sin(x)<0 donc x-sin(x)<x³/6 d'autre part.

Donc, en réunissant les inégalités (1) et (2) on peut dire que :

si x>0, alors 0<x-sin(x)<x³/6

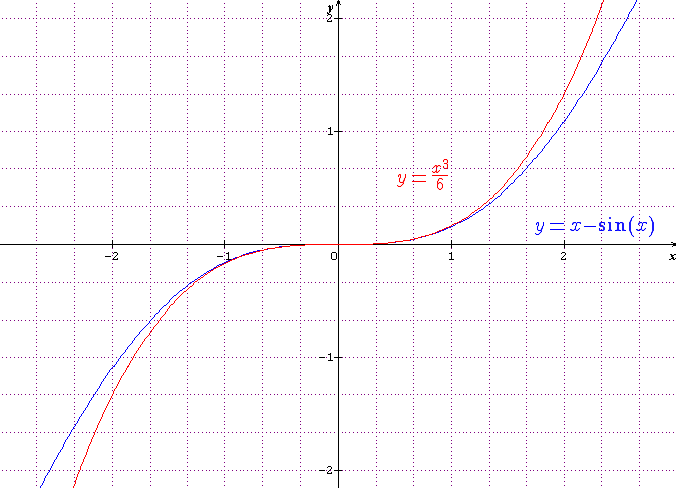
Remarque : sur le dessin ci-dessous, on constate bien que, à droite de l'axe Oy (lorsque x>), la courbe bleue (d'équation y=x-sin(x)) est entre l'axe Ox (d'équation y=0) et la courbe rouge (d'équation y=x³/6).
C'est la même chose lorsque x<0 : la courbe bleue est entre l'axe Ox et la courbe rouge, ce qui se traduit par :
si x<0 alors x³/6<x-sin(x)<0



*** message déplacé ***