Inscription / Connexion Nouveau Sujet
fonction derivée 2
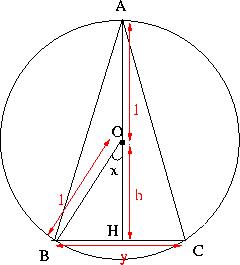
Un triangle ABC isocele, de sommet principal A, est inscrit dans un cercle de centre O et de rayon 1 comme la figure ci-apres.
Soit x la mesure en radians de (OH;OB)telle que 0 plus petit ou egale a x plu petit ou egale a pi/2.
1)Exprimer en fonction de x l'aire du triangle ABC.
2)a) Resoudre dans [0;pi/2] l'equation 2cos²x+cosx-1=0
b)Etudier le sens de variation de la fonction f definie sur [0;pi/2] par f(x)=(sinx)(1+cos x).
3)En deduire lavaleur de x pour laquelle l'aire du triangle ABC est maximale.
je remercie davance les personnes cpable de resoudre cet exercice
(1) Le dessin ne serait pas de trop... Où est H?
(2a) Petit tuyau: effectue le changement de variable suivant y=cos(x)
(2b) Rappelle-toi que
Isis
slt isis
alor (ah) est la hauteur du triangle ABC passant par A. commen faire pour poster un dessin?
Pour insérer une images tu cliques sur l'icône "montagnne" en bas du message.
Je crois que j'ai compris comment est ton image. Je pose y=BC, h=OH. Il faut remarquer que OA=OB=1.
L'aire du triangle isoscèle ABC est S=AH*BC/2=(h+1)y/2.
En regardant le triangle rectangle OBH on a h=cos(x) et y/2=sin(x).
De là on reprend l'équation de l'aire: S=(h+1)y/2=(cos(x)+1)sin(x).
Isis
Meci bokoup IsiS pour cette aide recieuse .ayan chercher la reponses a laquesion 2 je tourne en rn d et ne trouve rien je desepere .sinon le schema est le meme sof keds mon exo le B est la place du C mai sa revien o  meme
meme
La question 2? Pour le (a) il faut faire le changement de variable suivant y=cos(x), c'est-à-dire que tu remplaces les cos(x) par y, tu résouds l'équation du 2ème dégré en y, puis tu en déduits les valeurs de x en reprenant y=cos(x).
Pour le 2b il faut se rappeler de 3 choses:
(sin(x))'=cos(x)
(cos(x))'=-sin(x)
(f(x)g(x))'=f'(x)g(x)+f(x)g'(x)
Le c est facile si t'as réussi le 2b. Il suffit de poser f'(x)=0 et trouver les x qui font que l'aire est extrémale (maximale ou minimale).
Isis
pour a kestion 2a je trouve
cosx =  ((1-cos(x))/2
((1-cos(x))/2
c sa ? merci de ton aide


