Inscription / Connexion Nouveau Sujet
fonction dérivée
Bonjour,
Voilà, j'ai un devoir maison à faire en math, je rencontre un problème dans un exercice et je voudrais que vous m'aidiez a me faire comprendre comme le résoudre.
Voici un scan de l'exercice.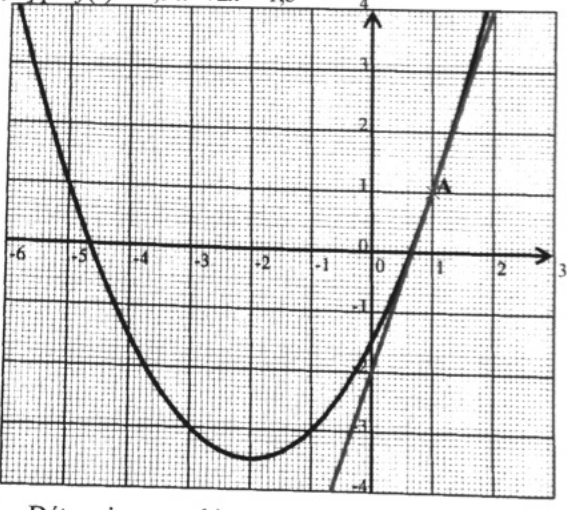
* Tom_Pascal > image placée sur le serveur de l' , merci d'en faire autant la prochaine fois Vitoria21 *
, merci d'en faire autant la prochaine fois Vitoria21 *
* Tom_Pascal > Image recadrée, sur la figure uniquement ! Si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum *
Merci de votre aide.
Bonsoir Vitoria21
Tu devrais savoir que les scans d'énoncé ne sont pas permis.
Qu'as-tu déjà trouvé comme réponses ?
Mais avant de répondre, Tom_Pascal a bien demandé que tu recopies ton énoncé.
Alors, j'attendais... désespérément qu'il apparaisse. 
Tu pourras être aidée quand il sera recopié.
Ah j'avais pas vu ! Désolé !
Voici l'énoncé :
On donne la représentation graphique de la fonction f définie sur l'intervalle [-6;3] par : f(x) : 0.5x² + 2x - 1.5
1) Déterminez graphiquement f'(1) puis f'(-2)
2) a. Déterminez l'expression de la fonction dérivée f'
b. Déterminez f'(-3)
3) Déterminez les coordonnées du minimum de la fonction f.
4) Dressez le tableau de variation de la fonction f sur [-6;3]
Parfait 
représente le coefficient directeur de la tangente au graphique représentant la fonction f au point de coordonnées (a ;f(a)), si cette tangente existe et n'est pas parallèle à l'axe des ordonnées.
Concernant , il faudra déterminer le coefficient directeur de la tangente au point A.
Cette tangente passe par les points (1;1) et (0;-2).
Que vaut ce coefficient directeur ?
Petit rappel :
Si A(xA;yA) et B(xB;yB), alors un coefficient directeur de la droite (AB) est égal à
Merci c'est sympa de ta part de m'avoir aider pour cette question mais je suis bloquer à la 2.b , j'aurais penser à une fonction constante mais je suis pas du tout sur, tu peux essayer de m'éclairer ?
Merci.
Non, ce n'est pas ça du tout... 
Mais quand je parlais de la suite, je voulais toujours rester à la question 1.
1) Déterminez graphiquement f'(1)
f(x) = 0.5x² + 2x - 1.5
f'(x) = 2 * 0.5x² + 2
f'(x) = 1x² + 2 ?
L'autre j'étais a l'ouest , je l'admet




