Inscription / Connexion Nouveau Sujet
Fonction dérivée
On considère la fonction f définie sur [ -2 ; 7 ] par :
f(x) = (1 / 3) x^3 - 3 x^2 + 5x + 8
Sur tableur, on a obtenu le tableau de valeurs de la fonction f pour les entiers de - 2 à 7, ainsi que les valeurs de la dérivée.
1.a) Parmi les formules suivantes, indiquer celle qui, saisie en A3, permet, par recopie vers le bas, d'obtenir les entiers de - 1 à 7 :
= $A2+1 =$A$2+1 = -2+1
b) Dans la formule à saisir en B2, deux erreurs ont été faites:
= 1/(3*A2)^3+(-3)*A2+5*A2+8
Les retrouver.
c) La formule saisie en C2 est :
= A2^2+(-6)*A2+5. Est-ce correct ?
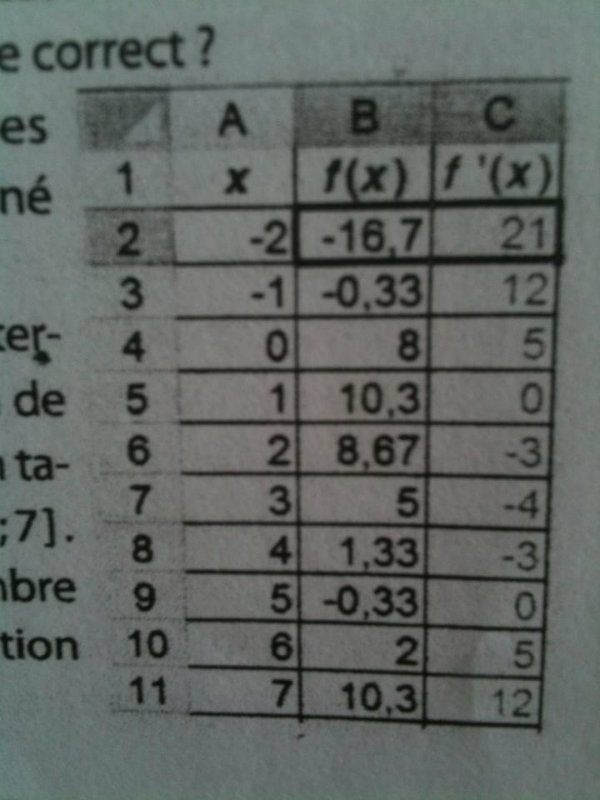
2. Le tableau corrigé des valeurs obtenues est donné ci-contre.
javascript:void(0) (en dessous)
Utiliser ce tableau pour déterminer le sens de variation de la fonction f et dresser son tableau de variation sur [-2 ; 7].
A priori, quel est le nombre de solutions de l'équation f(x) = 0 ?
Déjà, à la question 1.a) j'ai mis que c'était la première solution après avoir essayer les deux autres qui ne marchaient pas
A la question b)
j'ai supprimé le *A2 après le (-3) pour garder le chiffre négatif
est-ce bon déjà ?
il faut que cela revienne à taper ceci
f(x) = (1 / 3) x^3 - 3 x^2 + 5x + 8
A la question b)
j'ai supprimé le *A2 après le (-3) pour garder le chiffre négatif
est-ce bon déjà ? Afin d'obtenir le chiffre négatif du tableau qui est "-16,7"
non, c'est du bidouillage ça...
tu peux aussi tester sur un tableur...
tout à fait
ensuite x^3
tu dois regarder dans ton tableur où est mis la valeur de x
et savoir que tu veux ensuite tirer ta formule vers le bas
la valeur de x est en A1
je crois avoir trouvé !
Il faut changer le A2 en A1 n'est ce pas ?
Mais quand je met :
= (1/3)*A1^3+(-3)*A1+5*A1+8
Il y a un problème car dans ma formule, je trouve -3x et non -3x^2 comme dans la fonction f définie si je la calcule de tête
et sur mon tableur excel il m'indique " #VALEUR!" quand j'entre ma formule
non x est bien en A2 lorsque toi tu es en B2
la seconde erreur, c'est qu'ils ont oublié l'exposant 2 pour le -3x²
En A2 sur le tableau c'est -2, je ne comprends pas pourquoi vous dîtes que c'est x alors que sur le tableau (la photo donnée) il est en A1..
en A1, ils ont mis x pour dire qu'en dessous, on allait mettre les valeurs de x
mais la 1re valeur numérique de x est -2, qui est écrit en A2
Je trouve le résultat exact en B2 en ayant comme formule :
= (1/3)*A2^3+(-3)*A2^2+5*A2+8 vous avez bien raison, je viens de comprendre pourquoi nous devons prendre -2
le -2 remplace le x ce qui fait que le -2 remplace le x également dans la fonction f'(x)
ai-je raison ?
Pour la question c)
j'ai vérifié et oui la formule "=A2^2+(-6)*A2+5" est correct et on peut aussi la recopier vers le bas 




