Bonjour,

Pour la première question, il suffit de faire un tableau de signes (après avoir factorisé f(x)).
Tu as au moins fait cette question ?

Bonjour,
Pour la première question je pense que Patrice t'a bien guidé.
Pour la question 2, il suffit de dériver la fonction donnée, fais le avec la forme développée de f, c'est plus simple, puis étudier le signe de cette dérivée et ceci te permettra de faire un tableau de variation, ou tu mettras le signe de f' et les variation de f.
Commence déjà par ces deux questions et je t'aiderai au fur et a mesure pour le reste.
Bon courage !

Je ne suis pas encore très familier avec ce site donc pardonner de prendre en photo mes tableaux de signe.
1) J'ai donc factoriser x^3-x^2 ce qui m'a donné x^2 (x-1)
J'ai ensuite chercher les solutions
Et j'ai trouvé pour x^2=0 donc x=0 et x-1=0 donc x =1
J'ai ensuite mis ces valeurs dans mon tableau de signes.

2) j'ai  derivé la fonction ce qui m'a donné 3x^2 - 2x  et j'en ai déduit que c'était un polynôme du 2nd degré du coup j'ai calculé delta que j'ai trouvé égal à 4 puis j'ai trouvé comme solution 0 et 2/3.

Je voudrais savoir si mon raisonnement jusqu'ici est bon et si tout est juste.
Cordialement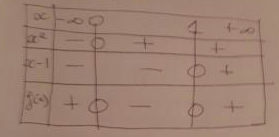



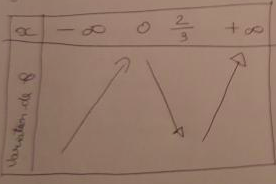
***image recadrée***le reste doit être recopié***

***citation inutile supprimée***

Désolé d'avoir reposé je ne suis pas encore habitué

*reposté

Il y a une erreur dans ton tableau de signes : le signe de x² est positif sur toute la ligne (un carré est toujours positif ou nul).

Pour le tableau de variation, c'est correct. Il faudrait simplement calculer les valeurs f(0) et f(2/3).

D'accord donc si j'ai bien compris mon tableau de signe ne doit avoir qu'une seule solution, en l'occurrence 1

Non, il y a bien 2 valeurs qui annulent f(x) (0 et 1) mais le facteur x² est toujours positif ou nul...

Mais qu'est ce que je devrais faire concrètement pour corriger mon tableau. Mettre que des plus pour x^2

Il faut que tu corriges ton tableau de signe de f. Sur la ligne de x^2 il faut que tu mettes des + partout et le 0 tu le laisses car un carrée est toujours positif ou nul. Donc la ligne de f' va également changer,  de - l'infini à  0, il faut changer le + par un -
Pour ton tableau de variation il faut mettre la ligne du signe de f' et par la suite les variations de f qui finalement ont été obtenues grâce au signe de f'.

L' équation de la tangente a la courbe C au point d'abscisse 2 est donnée par
y= f'(x)(x-2) + f(2)   la formule générale doit être dans ton cours
Il suffit de calculer f(2) et f'(2) et les remplacer dans l'équation.

Bonjour je reviens pour la question 1
Est-ce juste.

Voilà la question 1

Cette fois c'est bon

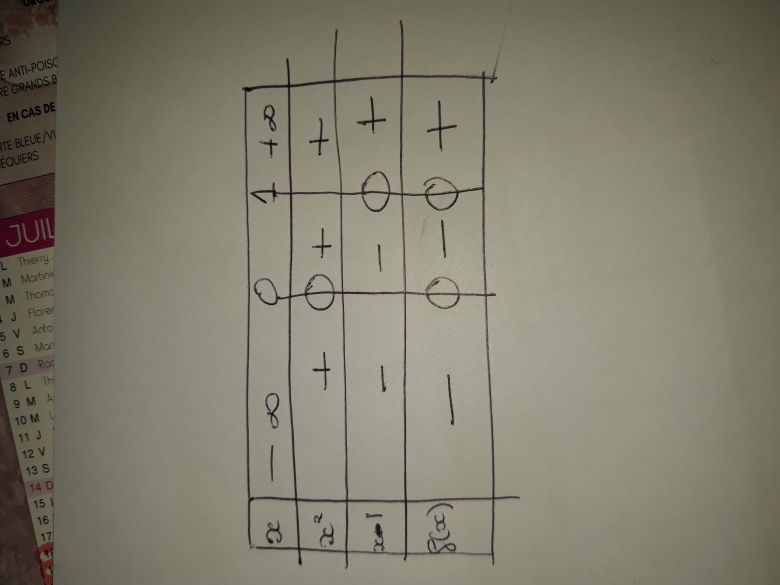
Pour la question  2 j'ai donc calculer la dérivée  j'ai trouvé  3x^2- 2x  j'en ai déduit que c'est un polynôme du 2nd degré  j'ai trouvé un delta de 4 et comme  solution  0 et 2/3.  J'ai rempli mon tableau avec le signe de la dérivée puis la variation de f
Est-ce juste ?

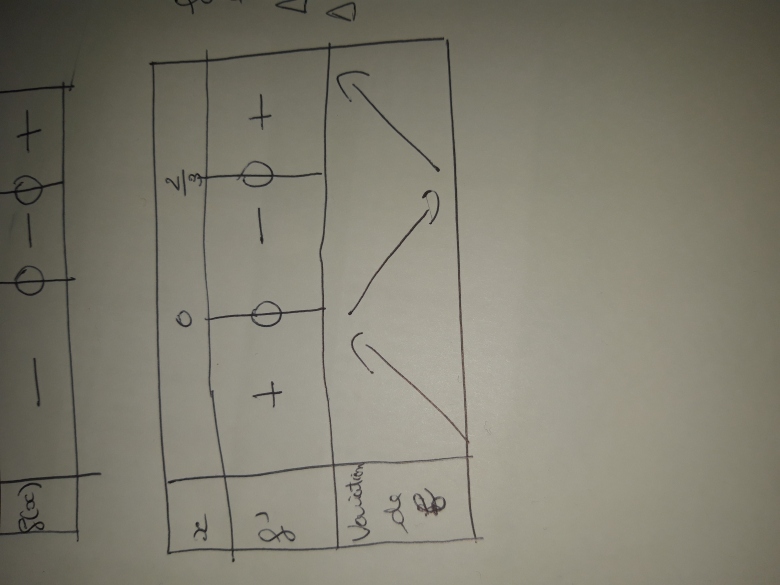
Et pour les images du tableau de variation j'ai trouvé pour 0, 0 j'ai remplacé  dans l'expression de départ les x
0^3 -0^2 =0
Et Pour 2/3 j'ai fait de même
2/3^3 - 2/3^2 = -4/27

En attendant une réponse pour la question 2, je me suis avancé sur la question  3. J'ai donc utilisé la formule f'(2) (x-2) + f(2) avec a =2
Pour trouver f'(2) j'ai remplacé les x par 2 dans la dérivée
3×2^2-2×2 =    8
Et pour f(2) j'ai remplacé dans l'expression de départ
2^3-2^2 =       4

J'ai remplacé le tout dans la formule
y = 8 (x-2) +4
y = 8x -12
Voilà  j'ai trouvé ce résultat mais je ne sais pas si c'est juste.

Oui les images que tu viens de trouver sont justes. Il ne faut oublier de les mettre dans ton tableau de variation

D'accord merci et pour la tangente à la question 3.

Oui l'equation de la tangente que tu viens de trouver est juste.

Pour la question 3 il faut dériver g faire un tableau de variation avec le signe de g' et les variations de g, comme tu l'as déjà fait pour f

Désolée je voulais dire pour la question 4

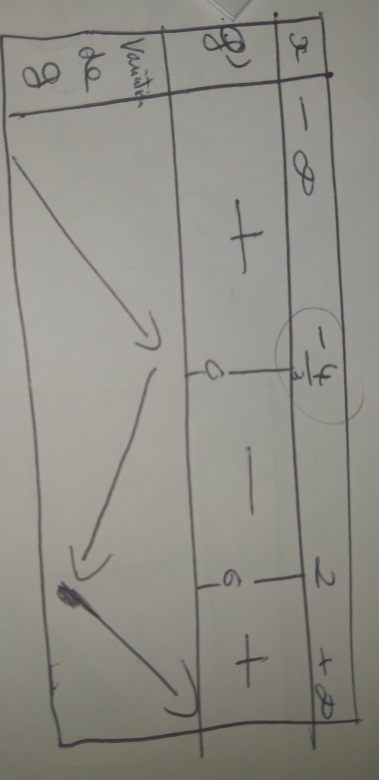
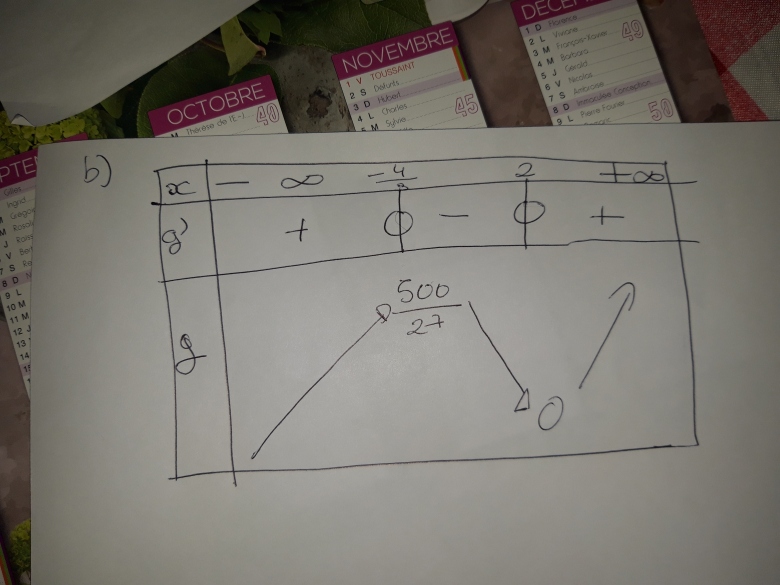
Pour la question 4 a)
J'ai  calculé la dérivée de x^3-x^2-8x +12
Ce qui m'a donné 3x^2- 2x -8
J'ai calculé le delta que j'ai trouvé de 100 et les solutions que j'ai trouvé : -4/3 et 2
Après j'ai  calculer leur images en remplaçant dans l'expression de départ ce qui m'a donné pour -4/3
-4/3^3+4/3^2-8×-4/3+12
=596/27         ( résultat que je trouve bizarre)
Et pour 2 j'ai fait la même chose et j'ai trouvé  0.
Je doute sérieusement de mes résultats pour le coup.

Je trouve ce tableau de variation je n'ai pas mis les images car je pense qu'elles sont fausses. Besoin de votre aide.

C'est bon j'ai  compris mon erreur ce n'est pas 596/27 mais 500/27

Voilà donc mon tableau de variation
Pouvez vous me dire ce que je dois faire à la question 4 b et la c.