Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. PremièreForum de première DérivationTopics traitant de dérivation [tout]Lister tous les topics de mathématiques

1 2 +

Posté par Profil Devoirs33re : Fonction dérivées 26-10-21 à 14:27

J'ai essayé de faire ceci :
f'(x) = f'(a)
f(x) = f(a)

y = f(a) + f'(a) (x-a)
y= (4x² + 8x + 49) + (8x+8) (x-4x² + 8x + 49)
Je trouve : -32x^{3} + 44x² + 472x + 441

Posté par
heklare : Fonction dérivées 26-10-21 à 14:30

Bonjour


Non f'(x)=8x+8
lorsque vous avez écrit l'équation de la tangente vous avez écrit

f'(2)=8\times 2-8

Au point d'abscisse a le problème est le même f'(a)=
f(a)= ?

Posté par Profil Devoirs33re : Fonction dérivées 26-10-21 à 14:36

Pourquoi f'(2) ?

Et, on devrait trouver f'(2) = 8* 2 + 8 = 24 ?

Posté par
heklare : Fonction dérivées 26-10-21 à 14:45

Désolé quelques erreurs
c'était un exemple pour montrer que ce n'était pas ce que vous aviez fait avant lorsque vous calculiez le nombre dérivé en un point

si j'ai f'(x)=8x+8  pour avoir f'(2) par exemple je

vais remplacer x par 2 ce qui donne bien ce que vous avez écrit

f'(2)=8\times 2+8=24

Si je veux maintenant f'(a) je vais donc remplacer x par a

Posté par
malou Webmasterre : Fonction dérivées 26-10-21 à 14:45

hekla @ 26-10-2021 à 14:30

Bonjour


Non f'(x)=8x+8
lorsque vous avez écrit l'équation de la tangente vous avez écrit

f'(2)=8\times 2{\red{+}}8

Au point d'abscisse a le problème est le même f'(a)=
f(a)= ?

Posté par
heklare : Fonction dérivées 26-10-21 à 14:48

Bonjour malou

Oui j'ai rectifié l'erreur

Posté par Profil Devoirs33re : Fonction dérivées 26-10-21 à 14:49

Donc, f'(a)= 8a + 8 ?

Posté par
malou Webmasterre : Fonction dérivées 26-10-21 à 14:55

oui, calcule f(a) également maintenant

Posté par Profil Devoirs33re : Fonction dérivées 26-10-21 à 14:56

f(x) = 4x² + 8x + 49

f(a) = 4a² + 8a + 49  normalement.

Posté par
malou Webmasterre : Fonction dérivées 26-10-21 à 14:58

parfait

maintenant tu remplaces dans y= f(a) + f'(a)(x-a)

Posté par Profil Devoirs33re : Fonction dérivées 26-10-21 à 15:09

y= f(a) + f'(a) (x-a)
y= (4a²+8a+49) +(8a+8)(x-4a²+8a+49)
Pour l'instant, c'est cela ?

Posté par
malou Webmasterre : Fonction dérivées 26-10-21 à 15:12

Devoirs33 @ 26-10-2021 à 15:09

y= f(a) + f'(a) (x-a)
y= (4a²+8a+49) +(8a+8)\strike{{\red{(x-4a²+8a+49)}}}
Pour l'instant, c'est cela ?


pas ce qui est en rouge...
tu avais (x-a)
tu dois le garder ! aucune raison de le changer

Posté par Profil Devoirs33re : Fonction dérivées 26-10-21 à 15:15

d'accord,
je trouve : y = -4a² + 49 + 8a x + 8x

Posté par
malou Webmasterre : Fonction dérivées 26-10-21 à 15:18

bien, oui que tu peux aussi écrire,

y=-4a²+49+(8a+8)x

qui est, dans cette équation de droite, la constante maintenant qui doit être nulle pour être sur que la droite passe par l'origine ?

Posté par
heklare : Fonction dérivées 26-10-21 à 15:20

Puisque c'est une équation de droite il vaut mieux la garder sous la forme y= mx+p

y=(8a+a)x+(8a+8)\times 8+4a^2+8a+49

malou edit ** ceci est faux ** j'ai remis la vraie réponse plus bas **

Posté par Profil Devoirs33re : Fonction dérivées 26-10-21 à 15:20

la constante qui doit être nulle pour être sur que la droite passe par l'origine est 8 ?

Posté par
heklare : Fonction dérivées 26-10-21 à 15:21

Bon j'arrête je finis par écrire n'importe quoi

Posté par
malou Webmasterre : Fonction dérivées 26-10-21 à 15:22


Devoirs33 @ 26-10-2021 à 15:20

la constante qui doit être nulle pour être sur que la droite passe par l'origine est 8 ?

non

malou @ 26-10-2021 à 15:18

bien, oui que tu peux aussi écrire,

y=-4a²+49+(8a+8)x

qui est, dans cette équation de droite, la constante maintenant qui doit être nulle pour être sur que la droite passe par l'origine ?


la constante, dans une équation de droite, c'est tout ce qui n'est pas en facteur de x

donc quelle est la constante ici ?

Posté par Profil Devoirs33re : Fonction dérivées 26-10-21 à 15:26

Il y a deux expressions qui ne sont pas en facteur de x.

-4 et 49

Posté par
malou Webmasterre : Fonction dérivées 26-10-21 à 15:28

non, il n'y a qu'une seule expression qui n'est pas en facteur de x
c'est
-4a²+49

il faut te dire que a est un nombre comme un autre, certes pour le moment, tu ne connais pas sa valeur, mais c'est un nombre

donc cette constante -4a²+49 doit être nulle, pour être sur que tes droites passent par l'origine du repère
tu dois donc résoudre
-4a²+49=0

à toi

Posté par Profil Devoirs33re : Fonction dérivées 26-10-21 à 15:35

je trouve 2 solutions

-3,5 et 3,5

Posté par
heklare : Fonction dérivées 26-10-21 à 15:58

Oui x= \pm \sqrt{\dfrac{49}{4}}=\pm \dfrac{7}{2}

Posté par
malou Webmasterre : Fonction dérivées 26-10-21 à 16:09

très bien

vois ce dessin de la situation
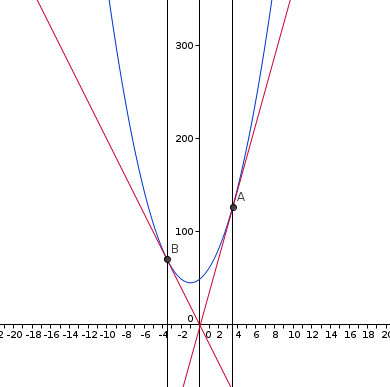
Fonction dérivées

tu vois que tu as A d'abscisse 3,5 et B d'abscisse -3,5
et que les tangentes à la courbe en ces points (en rouge) passent bien par l'origine du repère

Posté par Profil Devoirs33re : Fonction dérivées 26-10-21 à 16:19

Merci beaucoup pour votre aide hekla et malou.

Bonne journée.

Posté par
heklare : Fonction dérivées 26-10-21 à 17:31

De rien.  C'est juste pour changer la couleur du carton en bleu

1 2 +


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !