Inscription / Connexion Nouveau Sujet
Fonction dérivées
 Devoirs33
Devoirs33Bonsoir à tous,
J'aimerai de l'aide/corrections pour cette exercice s'il vous plaît . Merci.
Exercice 1 :
a) Soit f une fonction représentée par la courbe en pièce jointe.
Déterminer graphiquement l'équation de la tangente à C au point d'abscisse −2.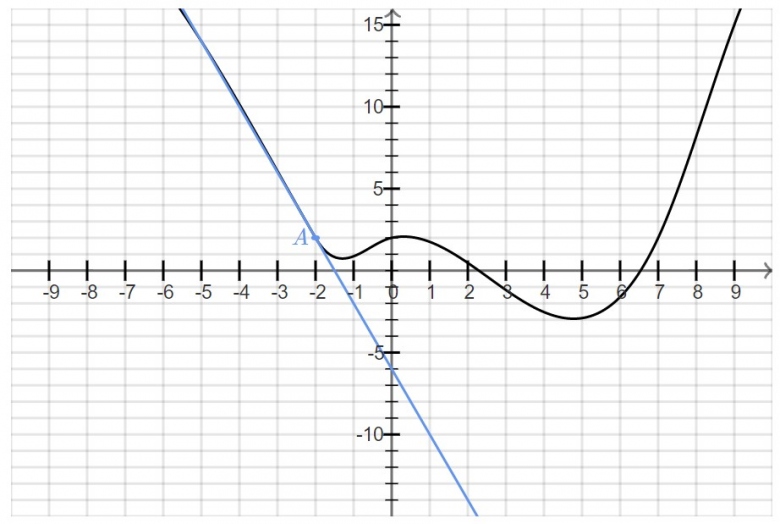
Je cherche le coefficient directeur.
A ( -2 ; 2) et B (-1,5 ; -6)
a = (-6 -2) / (-2-(-1,5) = 16
équation : y = ax + b
y = 16x - 6 ?
b)Je cherche le coefficient directeur
A ( -7 ; 6) et B ( ; )
y = ax+b
c)Soit f une fonction représentée par la courbe C.
f(x) = 5−6x²−8xCalculer la dérivée f'(x) de f. On admettra qu'elle est dérivable sur R.
f(x) = 5 - 6x² - 8x
On pose u(x) = -6x² u'(x) = -6*2x = -12x ( fonction carrée 2x)
On pose v(x) = -8x+5 v'(x) = -8 (fonction affine ax+b=a)
f'(x) = -12x - 8
Ensuite, déterminer l'abscisse du point de la courbe C dont la tangente possède un coefficient directeur égal à -2.
d)Calculez la dérivée f'(x) de f. On admettra qu'elle est dérivable sur R.
f(x) =4x²+8x+49
On pose u(x) = 4x² et v(x) = 8x+49
u(x) = 4x² u'(x) = 4*2x = 8x
v(x) = 8x + 49 v'(x) = 8
f'(x) = 8x+8
e)Déterminer une équation de la tangente à la courbe représentative de la fonction f définie sur R par f(x) = 9x² + 4x −5 au point d'abscisse -2.
(oubli de pièce jointe + énoncé)
b)Déterminer graphiquement l'équation de la tangente à C au point d'abscisse-7 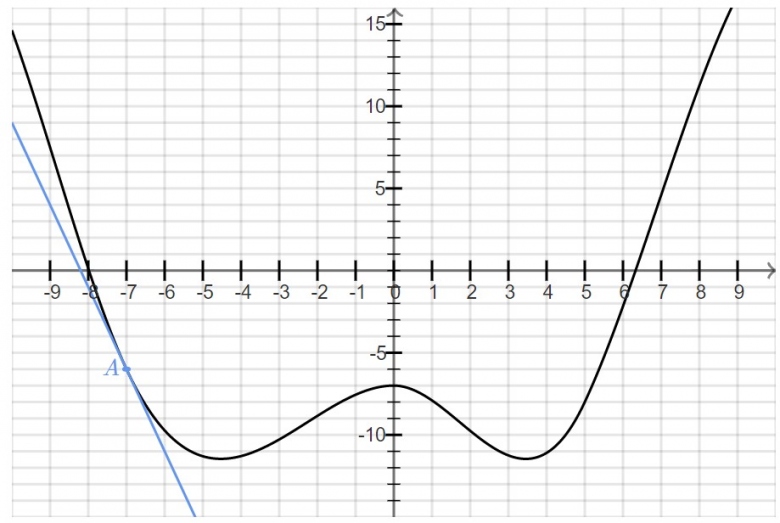 .
.
Bonsoir
en attendant que quelqu'un te vienne en aide, corrige déjà ça, et refais le (droite qui "descend "....tu ne peux pas trouver un coefficient directeur positif ! )
B est faux
quelle est l'abscisse du point de l'axe des ordonnées qui a pour ordonnée -6 ?
N'y a t-il pas un mélange des questions ?
b) Soit f une fonction représentée par la courbe C.
Déterminer graphiquement l'équation de la tangente à C au point d'abscisse-7 et la courbe est la deuxième image
Pour B prendre un nœud de quadrillage 2 points répondent à la question
Non, il n'y a pas de mélange des questions.
Je constate que -6 est l'ordonnée à l'origine car la droite A coupe l'ordonnée en -6.
Pour choisir B, on choisit 2 points au hasard se situant sur la courbe ?
Un seul point puisque vous avez déjà le point de tangence
Au hasard, si vous voulez, mais un nœud de quadrillage est quand même plus facile
d'accord merci.
b)A ( -7 ; 6) et B ( 0; -6)
'-6-6)/(0-6)=2
y = ax+b
y= 2x + b comment déterminer b alors que la tangente ne coupe pas l'ordonnée ?
Question a) premier graphique
le point de tangence A
Autre point : on choisit l'intersection avec l'axe des ordonnées
B
Conclusion équation de la tangente
Question b) deuxième graphique
Point de tangence oubli du signe
Second point on choisit
Qu'avez-vous fait pour trouver 2 ?
La remarque est encore valable : on ne peut pas trouver un coefficient positif si la droite « descend »
Vous n'aviez pas pris les bonnes valeurs, en outre 6-6=0
D'accord pour -5 Pour trouver l'ordonnée à l'origine
écrivez que cette droite passe par A
Absolument pas
Un point appartient à une courbe si et seulement si ses coordonnées vérifient l'équation de la courbe
Équation de la courbe
Passe par A :
Vous connaissez tout sauf
c'est la première fois que je rencontre un exercice de ce type.
Je ne suis vraiment pas sûre de moi, mais je suppose qu'on doit résoudre une équation afin de trouver l'ordonnée à l'origine qu'on ne peut pas lire graphiquement.
On a donc :
yA = a xA + b
=> b = yA - a xA
b = -6 - (-7) = 1
Autrement, je ne vois pas comment déterminer l'ordonnée à l'origine.
Absolument
C'est une conséquence du covid que vous n'avez pas vu cela l'an dernier lors des équations de droite
c) d'accord pour une équation à résoudre
Ah d'accord. Je trouve que c'est une notion importante à aborder, merci de me l'avoir fait découvrir.
c) Déterminer l'abscisse du point de la courbe C dont la tangente possède un coefficient directeur égal à -2.
Comment suis-je sensée faire pour trouver l'abscisse d'une tangente ?
Vous avez d'une manière générale le coefficient directeur de toutes les tangentes.
Il est fonction de . On vous demande donc pour quelle valeur de
ce coefficient directeur vaut
Bien sûr, vous avez le coefficient directeur au point d'abscisse
il vaut ; On veut donc savoir si l'on peut trouver un
pour qu'il vaille
e) Tout d'abord, je calcule le taux de variation.
pour l'instant c'est correct ?
ensuite je calcule l'équation de la tangente à l'aide du taux de variation.
y= f'(a) (x-a)+f(a)
Pourquoi faire simple quand on peut faire compliqué.
Vous venez de passer du temps à écrire les fonctions dérivées ; pourquoi vous ne vous en servez pas ?
Vous avez oublié de mettre au carré première ligne
Vous ne revenez à la définition uniquement si vous ne pouvez pas faire autrement
Dorénavant, c'est pour l'équation d'une tangente
Afin de trouver l'équation de la tangente.
Ne fallait-il pas faire cela ?
Y'avait - il un moyen plus pertinent que celui-ci ?
J'ai suivi la méthode d'un exercice qu'on avait fait auparavant.
Je pensais que c'était cette méthode qu'il fallait suivre.
Oui je vous l'ai écrit à 22 : 44
d'où
Ce que vous auriez trouvé en poursuivant
équation de la tangente
On est bien d'accord.
Pour écrire l'équation de la tangente en un point, il nous faut le nombre dérivé en ce point.
Maintenant on le récupère en écrivant la fonction dérivée. Ce n'est pas la peine de réinventer la roue à chaque fois
Le travail a été fait une bonne fois pour toutes, pour un certain nombre de fonctions bien régulières. Il faut garder la limite du taux d'accroissement pour les fonctions un peu exotiques présentant certaines particularités.
D'accord, merci infiniment pour votre aide, ainsi que vos conseils.
J'ai à présent, compris la plupart des exercices, et saurai les refaire grâce à vous. Je suis ébahie par votre passion : les mathématiques.
Bonne nuit.
A une prochaine fois.
Bonjour,
J'ai oublié une autre question dans l'exercice d).
d)Calculez la dérivée f'(x) de f. On admettra qu'elle est dérivable sur R.
f(x) =4x²+8x+49
On pose u(x) = 4x² et v(x) = 8x+49
u(x) = 4x² u'(x) = 4*2x = 8x
v(x) = 8x + 49 v'(x) = 8
f'(x) = 8x+8
Ensuite, déterminez l'ensemble des abscisses des points pour lesquels la tangente à la courbe C, en ces points, passe aussi par l'origine. La réponse finale devra être sous forme d'ensemble.
Je sais que : Afin que la tangente en un point passe par l'origine ( 0 ; 0 ), l'équation est de la forme y = ax + b dans lequel, l'ordonnée à l'origine b est nulle.
On a donc y = ax
Equation de la tangente : y= f(a) + f'(a)(x-a)
Je cherche x donc je remplace a par x ?
y = f(x) + f'(x) (x - x) ?
tu as la fâcheuse habitude d'appeler par la même lettre des choses différentes, donc tu ne peux pas t'en sortir comme ça
f'(x)=8x+8 très bien
laisse tomber cette histoire de l'équation de droite, tu le sais, mais tu ne l'écris surtout pas avec ces notations
et tu cherches a une abscisse tel qu'en ce point de la courbe d'abscisse a , la droite d'équation y= f(a) + f'(a)(x-a) passe par l'origine du repère
tu connais f'(x), donc que vaut f'(a) ?
tu connais f(x), donc que vaut f(a) ?
remplace ensuite dans y= f(a) + f'(a)(x-a)
développe tout
et termine en écrivant que la constante doit être nulle (car ta tangente doit passer par l'origine du repère)
cela va te donner le "a" que tu cherches
à toi, vas-y doucement en lisant bien ligne après ligne


