Bonjour,

°Etudier le signe de f' :

je cherche pour quel x le dénominateur s'annule :

7+ 4x = 0
4x = - 7
x= -7/4 = -1,75

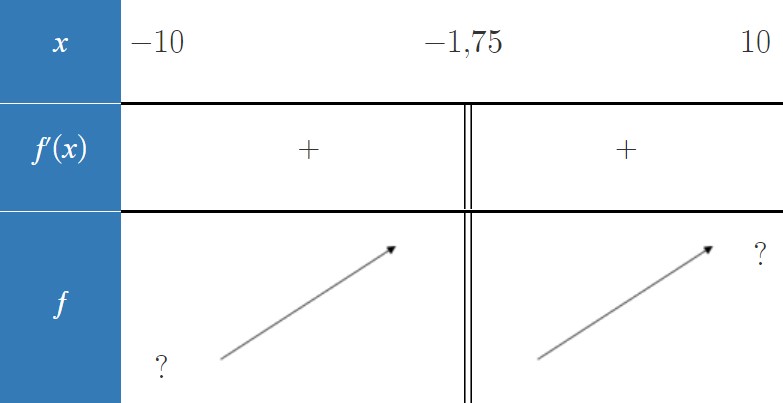
Dressons le tableau de signes :

x        |   -  -1,75  +
f'(x)  |            +                                  ||                            +

De passage

pour une fonction homographique

  sa dérivée

ici

Oui

Je n'ai pas encore vu cette propriété, merci de me l'avoir dit

Dressons le tableau de  variations :

x        |   - 10          -1,75    + 10
f'(x)  |            +         ||                +
f(x)   |  deux  flèche montante

pour trouver les extremums j'ai procédé ainsi :

f(-10) = 86/33
f(10) = 2

Normal puisque ce n'est jamais enseigné  
Cela fait pourtant gagner du temps

Il n'y a pas d'extrema  
si vous prenez une valeur proche de -7/4 alors à gauche vous aurez une valeur très grande positive et à droite une valeur très grande en valeur absolue mais négative

D'accord.
Donc que je dois mettre dans les ?

Là vous pouvez mettre ce que vous avez calculé 11 : 27, mais vous ne pouvez pas parler d'extremum

Bonjour : une remarque pour hekla ..

hekla D'accord merci beaucoup.
Dans ce cas, peut-on parler de " limites " ?

Oui, on parlera de limite quand tend vers à droite ou à gauche

Bonjour philgr22

Il fut un temps où il ne fallait pas en parler.

Il y a d'autres « astuces » qui ne sont plus enseignées

Soit une fonction définie par

Si est une valeur qui annule la dérivée alors

Je suis en retraite et on ne m'a jamais interdit de donner des "trucs" aux élèves. Ce n'est absolument pas du hors programme ,il faut savoir l'appliquer avec suffisamment de liberté....Il y a aussi le discriminanr reduit par exemple...et bien d'autres choses. Malgré tout ce qu'on peut dire, le prof a toujours une certaine liberté.