Inscription / Connexion Nouveau Sujet
Fonction dérivées
 Devoirs33
Devoirs33Bonsoir
Pouvez-vous m'aider pour cet exercice s'il vous plaît ?
Dresse le tableau de signes et de variations de la fonction suivante :
On pose u(x) = 50 --> u'(x) = 0
v(x) = 60/(x-6)² --> v'(x) = 60/(x-6)²
Je cherche pour quel x le dénominateur s'annule :
x- 6 = 0
x = 6 ( valeur interdite )
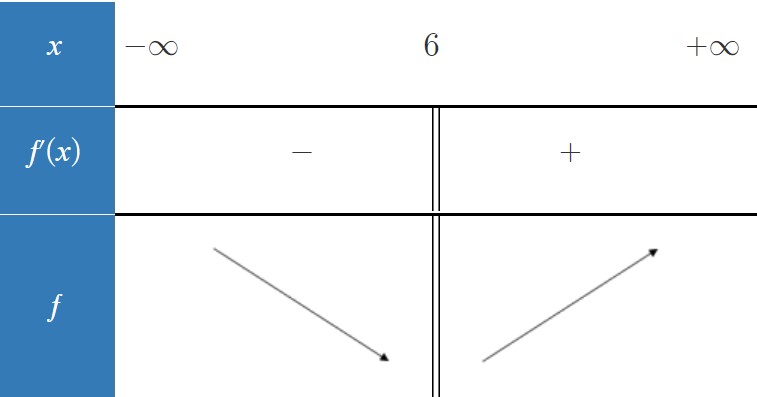
x | - 6 +
6 +
f'(x) | ||
f(x) |
est-ce correct pour l'instant ?
Non
si ou pour simplifier
en posant on a
Pourquoi écrivez-vous que la fonction est égale à sa dérivée ?
Si tu reflechis à la formule générale de la dérivée de u/v :
u'v -uv' devient -uv' pisque u' = 0 ,d'où la derivée de 1/v
Jusqu'ici j'ai compris mais en revanche, je n'ai pas compris pourquoi (x-6)^3 ?
Ce n'est pas (1/v)' = v' / v² ?
Bonjour à tous
Devoirs33, lis un peu ceci, ![]() A LIRE AVANT DE POSTER OU DE RÉPONDRE, MERCI
A LIRE AVANT DE POSTER OU DE RÉPONDRE, MERCI
en particulier la partie "Un rappel des règles plus particulières pour ceux qui désirent apporter de l'aide"
Je te remercie d'en tenir compte dorénavant dans tes demandes d'aide, qui s'adressent au site, et pas à une personne en particulier.
Bonsoir hekla : c'est penible de te voir toujours intervenir pour donner des reponses: ce n'est absolument pas pedagogique.Il vaut mieux laisser le temps de la reflexion aux eleves ,sinon aucun interet et ils ne progressent pas .
non, philgr22, tu ne fais pas doublon, tu as effectivement le droit de le dire
Les règles existent, et sauf abandon manifeste, ce qui n'est pas le cas ici, je pense qu'il est normal que tu râles un peu...tu poses des questions, et des réponses d'une autre personne arrivent entre temps...on ne peut pas gérer un sujet de la manière pour le bien de l'élève.
Comme je l'ai déjà dit je ne donne pas les réponses, mais quelques explications. Ce n'est pas en laissant mariner que ce sera plus pédagogique
D'autre part taper le texte en latex prend plus de temps
Bien sur devoirs 33 .
Hehla, les eleves actuels ont d'enormes difficultés en calcul et il est bon de leslaisser "mariner" (comme tu dis) seuls pour qu'ils voient leurs erreurs de methodes . Quand à la pedagogie , j'ai la pretention d'etre un bon pedagogue.
Sans rancunes.
Le correcteur automatique de cet exercice dit qu'il y a probablement une erreur, c'est pour quoi je vous ai posée la question.
Vous m'aviez pourtant dit que c'était correct, c'est pour cela que j'ai mit 6.
J'ai trouvé 6 grâce à une équation
Deux remarques qui peuvent t'aider pour les dérivées:
1) pense à la formule que je t'ai rappelée : kf a pour dérivée kf' si k est une constante. Elle te permet d'isoler les constantes multiplicatives et de les remettre apres tes calculs dans la derivée.
2) Dans la mesure où le but d'une dérivée est d'etudier son signe, pense ,si possible à factoriser et non à développer.
Oui c'est correct ; quands on dit valeur interdite, celà signifie qu'il n'y a pas d'image . Ici le calcul pour x=6 est impossible d'accord? Mais 6 existe comme valeur de x.
la dérivée est : f'(x) = -2/(x-6)^3
Je cherche la valeur de x pour laquelle le dénominateur s'annule
x- 6 = 0
x = 6
c'est comme ceci que j'ai trouvé 6 mais apparemment ce n'est pas correct donc je ne sais pas comment procéder.
Lre probleme est que la fonction n'est pas definie pour x=6 ( le denominateur d'une fraction de doit pas ....) donc la derivée non plus .
la fonction s'etudie sur ]- ;6[
;6[ ]6;+
]6;+ [
[
La consigne ne prévient pas le domaine de définition.
Seul solution, je trouve : 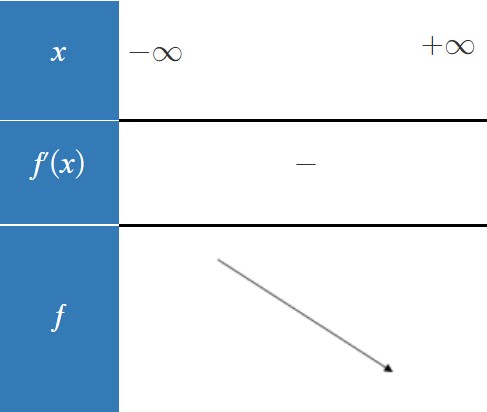
Autrement, je ne vois pas comment faire.
Pourquoi cette modification ? Ce que tu avais fait etait correct.
Verifie la courbe à la calculatrice .
J'ai modifié parce que le correcteur automatique n'accepte pas la réponse précédente contenant 6.
Etant donné qu'il ne précise pas le domaine de définition, et que vous proposez une en n'incluant pas 6, j'ai décidé d'enlever 6 du tableau.
Encore une fois f(x) n'existe pas pour x=6 . Donc tu es obligée de preciser cette valeur interdite des le depart.
Tu aurais eu une racine carrée à etudier , il aurait fallu etudier le signe du radical pour son ensemble de definition..D'accord?
J'ai modifié parce que le correcteur automatique n'accepte pas la réponse précédente contenant 6.
Etant donné qu'il ne précise pas le domaine de définition, et que vous proposez une en n'incluant pas 6, j'ai décidé d'enlever 6 du tableau.
Tu vois bien que ton tableau ne donne pas un sens de variation correct non?
De quel correcteur parles tu? Encore une fois ,ce que tu as fait à 18h38 est correct.Ta double barre montre bien que 6 n'a pas d'image.
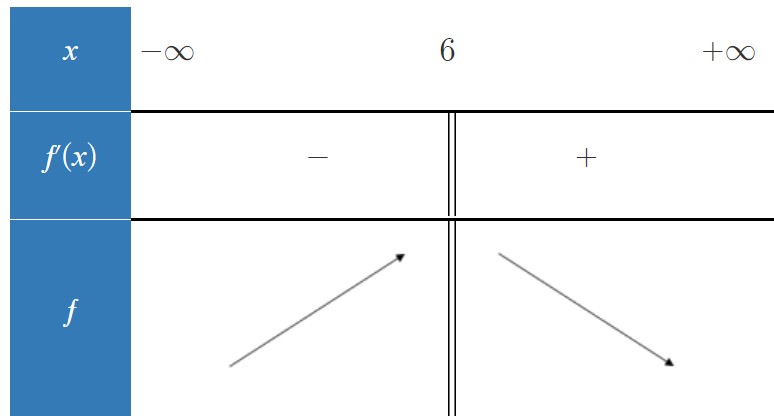
Non le tableau effectué contient des erreurs de signes.
C'était d'abord positif puis négatif.
Les flèches étaient donc montante puis descendante
Non le tableau effectué contient des erreurs de signes.
C'était d'abord positif puis négatif.
Les flèches étaient donc montante puis descendante
Non je t'ai dit à 18h38 et tu avais corrigé.