Inscription / Connexion Nouveau Sujet
Fonction exercice 1ere
Bonjour, je bloque totalement sur cet exercice depuis 4 jours... et j'ai finalement trouvé la solution de vous écrire pour avoir un peu d'aide...
Voici l'énoncé:
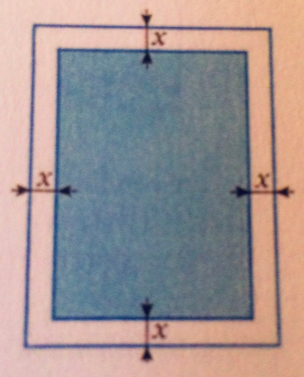
Une page rectangulaire de 20cm sur 30cm contient une zone imprimée (en bleu sur la figure) entourée d'en marges de même largeur.
On cherche quelles valeurs donner à la largeur x de la marge pour que l'aire de l'an zone imprimée soit supérieure à 459 cm2.
1) dans quel intervalle x varie-t-il ?
2) démontrer que le problème revient à résoudre l'inéquation 4x au carré -100x + 141 > 0
3) un logiciel de calcul formel donne: 4x au carré -100x + 141= (2x-3) (2x-47)
3A) vérifier le résultat fourni par le logiciel.
3B) faire le tableau de signe
3C) utiliser la question précédente pour résoudre dans l'ensemble des réels l'inéquation: 4x au carré -100x + 141 supérieur ou égal à 0.
4) En déduire la réponse au problème posé.
Je pense avoir malgré tout quelques idées.
Bonjour
peux-tu nous mettre la figure s'il te plaît...
et tu dis avoir quelques idées, écris les également
Le problème est que je n'arrive pas à joindre la figure!
Et oui voici mes idées pour la question 1:
Aire imprimée =aire totale de la feuille 20*30 =(600)-(aire des marges blanches) que je ne trouve pas !
Ensuite j'ai également réalisé l'inequation De la question 6 que je vous joint tout de suite:
4x au carré - 100x +141 est supérieur ou égal à 0.
A=4 B= -100 C=141
soit: (-100) au carré -4*4*141= 7744
donc: -100-racine carré de 7744 le tout divisé par 2*4
ce qui me donne 3/2
Puis : -(-100)+ racine de 7744 le tout divisé par 2*2
ce qui me donne 47
qu'en pensez vous ? malheureusement je n'arrive pas à poursuivre la forme factorisée certainement parce qu'il y a une erreur!
Enfin j'ai aussi fait mon tableau de signes que je vous montrerai a la fin.
Il serait plus simple de calculer la largeur du rectangle bleu ainsi que sa longueur
largeur 20 -2x longueur ? aire ?
question 3 développez (2x-3)(2x-47)
il n'est pas question du discriminant
tableau de signe ?
Pour moi l'aire du rectangle bleu est de 600 cm carré.
Mais je ne parviens pas à comprendre comment trouver cette intervalle précisément?
De plus, je suis qu'en première et je n'ai jamais entendu parler du discriminant désolé
600 est l'aire de toute la feuille
les dimensions doivent être positives cela donne des conditions sur
par exemple vous imprimez sur toute la largeur de la page donc ou vous ne laissez rien pour imprimer donc vous faites une marge de la moitié de la largeur de la page
vous avez calculé c'est bien ce que l'on a appelé le discriminant ou encore
Je viens de comprendre la question 2 qui est donc :
2×20X+2×30X-4×X^2 c'est à dire 100X-4X^2?
Mais je n'arrive pas à comprendre comment former l'intervalle pour la question 1 ? Pouvez vous m'aider s'il vous plaît. 
question 1
largeur de la feuille imprimée elle doit donc être positive quelles conditions sur
il est bien évident que la marge est positive donc
les deux vous donnent l'intervalle
aire du rectangle (20-2x)(30-2x)
pour le problème cette aire doit être supérieure à 459 d'où l'inégalité
à transformer pour obtenir ce que l'on vous demande
bonjour je pense avoir trouvé la réponse à la question 1;
pour cela j'ai fait (20-2x) (30-2x) supérieur ou égal à 0.
donc a=-2 et b=20 puis a=-2 et b=30.
ensuite j'ai réalisé le tableau de signe pour chaque expression.
et j'ai trouvé l'intervalle ]- infini;10] U [15;+infini [
est-ce juste ?
ah d'accord je pense avoir compris! je n'ai fait que des calculs inutiles encore une fois!
voici mon brouillon pour la question 2:
l'aire totale des marges vaut: 2*20x + 2*30x -4x au carré.
C'est à dire 100x-4x au carré
je pense etre de nouveau sur une mauvaise piste...
Vous donnez l'aire des marges mais ce que l'on veut est l'aire de la partie imprimable
soit aire totale aire des marges ou directement puisque l'on connaît les dimensions du rectangle imprimable
La partie imprimable est le rectangle bleu.
Le problème consiste à chercher les valeurs de rendant cette aire supérieure à 459
vous avez l'aire de la partie imprimable
On veut donc tq
Simplifiez et vous aurez répondu à la question 2
Si on regarde le dessin les marges représentent un contour formé de rectangles
Aire des 2 marges gauches et droites: rectangle de largeur x et de longueur 30 donc 2×X×30=60X
Aire des 2 marges hautes et basse: rectangle de largeur X et de longueur 20 donc 2×20X=40X
Mais On se rend compte que les coins carrés sont comptés en double donc il faudra enlever les 4 aires des 4 carrés de chaque coins (4×X^2)
Donc aire marges=60X+40X-4×X^2=100X-4X^2
Et donc aire zone imprimée =600-(100X-4X^2)=4X^2-100X+600
L'aire de la zone imprimée doit être supérieure à 459 donc
4X^2-100X+600>459 donne 4X^2-100X+141>0
est ce que cette réponse convient à la question 2 ?
Bien sûr
mais le calcul direct de l'aire du rectangle bleu est quand même plus rapide
ainsi que celui que vous avez préconisé au début aire du grand rectangle aire des marges
d'accord très bien.Le problème est que je n'arrivais pas à trouver comment calculer de manière rapide l'aire du rectangle bleu...
Pour la question 3a, j'ai simplement à montrer que quand on développe (2x-3) (2x-47) c'est égal à 4x carré-100x + 141 c'est bien ça que l'on me demande ?
Aire des 2 marges gauches et droites: rectangle de largeur x et de longueur 30 donc 2×X×30=60X
Aire des 2 marges hautes et basse: rectangle de largeur X et de longueur 20 donc 2×20X=40X
Mais On se rend compte que les coins carrés sont comptés en double donc il faudra enlever les 4 aires des 4 carrés de chaque coins (4×X^2)
Donc aire marges=60X+40X-4×X^2=100X-4X^2
Et donc aire zone imprimée =600-(100X-4X^2)=4X^2-100X+600
L'aire de la zone imprimée doit être supérieure à 459 donc
4X^2-100X+600>459 donne 4X^2-100X+141>0
est ce que cette réponse suffit pour la question 2 ? cette démonstration est correcte ?